Trắc nghiệm ôn tập chương 3 phần 2

Xét ΔABC có \(\dfrac{AC}{sinB}=2R\)

=>\(2R=\dfrac{6}{sin150}=12\)

=>R=6(cm)

=>Chọn C

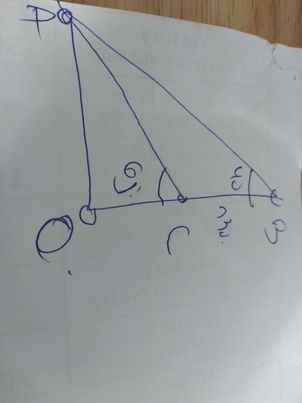
Kẻ AO vuông góc với BC tại O

=>OC là độ cao của ngọn đồi

\(\widehat{ACO}+\widehat{ACB}=180^0\)

=>\(\widehat{ACB}+65^0=180^0\)

=>\(\widehat{ACB}=115^0\)

Xét ΔACB có \(\widehat{ACO}\) là góc ngoài tại C

nên \(\widehat{ACO}=\widehat{CAB}+\widehat{CBA}\)

=>\(\widehat{CAB}+40^0=65^0\)

=>\(\widehat{CAB}=25^0\)

Xét ΔCAB có

\(\dfrac{BA}{sinACB}=\dfrac{BC}{sinBAC}\)

=>\(\dfrac{BA}{sin115}=\dfrac{130}{sin25}\)

=>\(BA=\dfrac{130}{sin25}\cdot sin115\simeq278,79\left(m\right)\)

Xét ΔBOA vuông tại O có \(cosABO=\dfrac{BO}{BA}\)

=>\(\dfrac{BO}{278.79}=cos40\)

=>\(BO=278,79\cdot cos40\simeq213,57\left(m\right)\)

BO=BC+CO

=>CO+130=213,57

=>CO=83,57(m)

Vậy: Độ cao của ngọn đồi là 83,57 mét

Câu 28: C

Câu 28: C

Chọn C

Chọn A

Chọn D

y = |x| là hàm chẵn nên đồ thị của nó nhận trục tung làm trục đối xứng

Chọn D

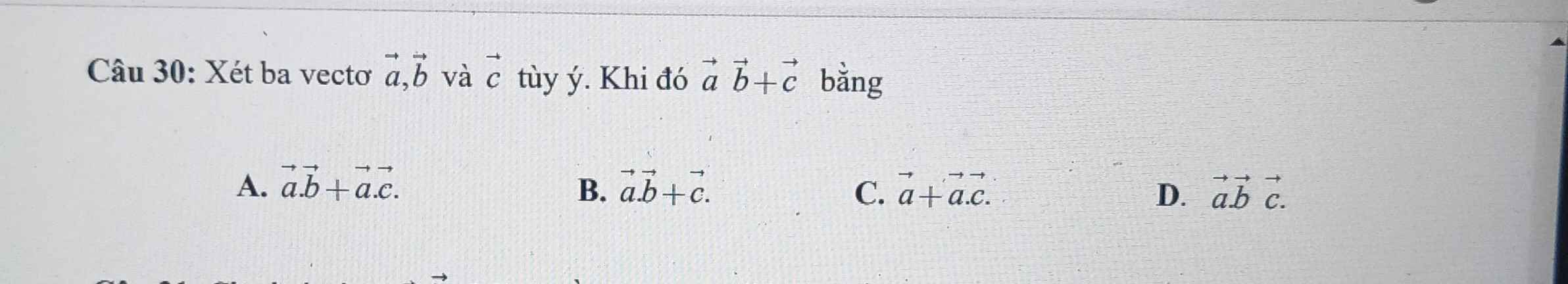
Ý C

\(\sqrt{\left(\left(xN-xM\right)^2+\left(yN-yM\right)^2\right)}\)·=\(\sqrt{\left(4-1\right)^2+\left(2+2\right)^2}\)  = 5

\(cos\left(B+C\right)=cos\left(180^o-A\right)=-cosA=-\dfrac{\sqrt{2}}{2}\Rightarrow cosA=\dfrac{\sqrt{2}}{2}\)

Định lí cosin: 

\(BC^2=AB^2+AC^2-2AB.AC.cosA\)

\(=2^2+\left(2\sqrt{2}\right)^2-2.2.2\sqrt{2}.\dfrac{\sqrt{2}}{2}=4\)

\(\Rightarrow BC=2\)