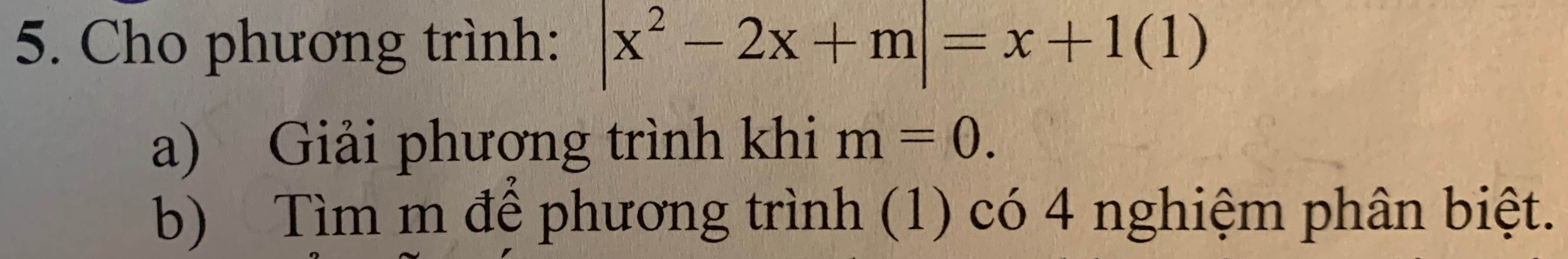
Hệ có chứa một phường trình đẳng cấp (thuần nhất)

Thay gốc tọa độ (0,0) vào BPT \(\Rightarrow0-0+7< 0\) không thỏa mãn

\(\Rightarrow\) Phần mặt phẳng không chứa gốc tọa độ (A hoặc C)

Do BPT ko chứa dấu "=" \(\Rightarrow\) không bao gồm đường thẳng (loại C)

Vậy A đúng

C

C

Câu C

ai giúp em vs

\(1,HPT\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)+\left(\dfrac{1}{y}-\dfrac{1}{x}\right)=0\\2y=x^3+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)\left(1+\dfrac{1}{xy}\right)=0\\2y=x^3+1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=y\\2y=x^3+1\end{matrix}\right.\\ \Leftrightarrow2y=y^3+1\Leftrightarrow y^3-2y+1=0\\ \Leftrightarrow\left[{}\begin{matrix}y=0\\y=\dfrac{-1+\sqrt{5}}{2}\\y=\dfrac{-1-\sqrt{5}}{2}\end{matrix}\right.\)

Vậy \(\left(x;y\right)=\left(0;0\right);\left(\dfrac{-1+\sqrt{5}}{2};\dfrac{-1+\sqrt{5}}{2}\right);\left(\dfrac{-1-\sqrt{5}}{2};\dfrac{-1-\sqrt{5}}{2}\right)\)

\(2,HPT\Leftrightarrow\left\{{}\begin{matrix}\sqrt{2\left(x^2+y^2\right)}+2\sqrt{xy}=16\\x+y+2\sqrt{xy}=16\end{matrix}\right.\\ \Leftrightarrow\sqrt{2\left(x^2+y^2\right)}=x+y\\ \Leftrightarrow\left(x-y\right)^2=0\Leftrightarrow x=y\\ \Leftrightarrow2\sqrt{x}=4\Leftrightarrow x=4\)

Vậy \(\left(x;y\right)=\left(4;4\right)\)

\(3,\text{Sửa: }\left\{{}\begin{matrix}\sqrt{x^2+3}+\left|y\right|=\sqrt{3}\left(1\right)\\\sqrt{y^2+5}+\left|x\right|=\sqrt{x^2+5}\left(2\right)\end{matrix}\right.\)

Ta thấy \(\sqrt{x^2+3}\ge\sqrt{3};\left|y\right|\ge0\Leftrightarrow VT\left(1\right)\ge\sqrt{3}=VP\left(1\right)\)

Dấu \("="\Leftrightarrow x=y=0\)

Thay vào \(\left(2\right)\Leftrightarrow\sqrt{5}+0=\sqrt{5}\left(tm\right)\)

Vậy \(\left(x;y\right)=\left(0;0\right)\)

\(\Delta'=\left(m+1\right)^2-\left(5m+1\right)=m^2-3m\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le0\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=5m+1\end{matrix}\right.\)

a.

\(S=\left(x_1+x_2\right)^2-3x_1x_2=4\left(m+1\right)^2-3\left(5m+1\right)\)

\(=4m^2-7m+1=\dfrac{7}{3}\left(m^2-3m\right)+\dfrac{5}{3}m^2+1\ge1\)

\(S_{min}=1\) khi \(\dfrac{7}{3}\left(m^2-3m\right)+\dfrac{5}{3}m^2=0\Rightarrow m=0\)

b.

\(1< x_1< x_2\Rightarrow\left\{{}\begin{matrix}\left(x_1-1\right)\left(x_2-1\right)>0\\\dfrac{x_1+x_2}{2}>1\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x_1x_2-\left(x_1+x_2\right)+1>0\\x_1+x_2>2\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}5m+1-2\left(m+1\right)+1>0\\2\left(m+1\right)>0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}m>0\\m>-1\end{matrix}\right.\) \(\Rightarrow m>0\)

Kết hợp điều kiện delta \(\Rightarrow m\ge3\)

\(a,\Leftrightarrow\Delta\ge0\Leftrightarrow\left(2m+2\right)^2-4\left(5m+1\right)\ge0\Leftrightarrow4m^2-12m\ge0\)

\(\Leftrightarrow\left[{}\begin{matrix}m\le0\\m\ge3\end{matrix}\right.\)

\(vi-ét\Rightarrow\left\{{}\begin{matrix}x1+x2=2m+2\\x1x2=5m+1\end{matrix}\right.\)

\(\Rightarrow S=x1^2+x2^2-x1x2=\left(x1+x2\right)^2-3x1x2\)

\(=\left(2m+2\right)^2-3\left(5m+1\right)=4m^2-7m+1\)

\(=\left(2m\right)^2-2.2.\dfrac{7}{4}.m+\left(\dfrac{7}{4}\right)^2-\dfrac{33}{16}=\left(2m-\dfrac{7}{4}\right)^2-\dfrac{33}{16}\left(1\right)\)

\(TH1:m\ge3\Rightarrow\left(1\right)\ge\left(2.3-\dfrac{7}{4}\right)^2-\dfrac{33}{16}=16\)

\(TH2:m\le0\Rightarrow\left(1\right)\ge\left(0-\dfrac{7}{4}\right)^2-\dfrac{33}{16}=1\)

\(\Rightarrow MinS=1\Leftrightarrow m=0\left(tm\right)\)

\(b,1< x1< x2\Leftrightarrow0< x1-1< x2-1\)

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\\left(x1-1\right)\left(x2-1\right)>0\\x1+x2-2>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>3\\m< 0\end{matrix}\right.\\\left[{}\begin{matrix}\left\{{}\begin{matrix}x1>1\\x2>1\end{matrix}\right.\\\left\{{}\begin{matrix}x1 < 1\\x2< 1\end{matrix}\right.\end{matrix}\right.\\2m+2-2>0\\\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>3\\m< 0\end{matrix}\right.\\\left[{}\begin{matrix}x1x2>1\\x1x2< 1\end{matrix}\right.\\m>0\\\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>3\\m< 0\end{matrix}\right.\\\left[{}\begin{matrix}m>0\\m< 0\end{matrix}\right.\\m>0\\\end{matrix}\right.\Rightarrow m>3\)

a, Với $m=0$ phương trình $(1)$ trở thành:

$|x^2-2x|=x+1$

\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x=x+1\\x^2-2x=-x-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2-3x=1\\x^2-x+1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}4x^2-12x+9=13\\\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\left(loại\right)\end{matrix}\right.\)

\(\Rightarrow\left(2x-3\right)^2=13\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{13}+3}{2}\\x=\dfrac{-\sqrt{13}+3}{2}\end{matrix}\right.\)

b, $pt(1)⇔$ \(\left[{}\begin{matrix}x^2-2x+m=x+1\\x^2-2x+m=-x-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2-3x+m-1=0\\x^2-x+m+1=0\end{matrix}\right.\)

Nên để pt (1) có 4 nghiệm phân biệt thì 2 phương trình trên phải có 2 nghiệm phân biệt tức $\triangle$ mỗi phương trình phải $>0$

tức là \(\left[{}\begin{matrix}\left(-3\right)^2-4.1.\left(m-1\right)>0\\\left(-1\right)^2-4.1\left(m+1\right)>0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4m< 5\\4m< -3\end{matrix}\right.\Leftrightarrow m< \dfrac{-3}{4}\)

Vậy $m<\dfrac{-3}{4}$ t/m đề 

ĐKXĐ: ...

Với \(\left[{}\begin{matrix}x=0\\y=0\end{matrix}\right.\) ko phải nghiệm

\(\Leftrightarrow\left\{{}\begin{matrix}2-\dfrac{1}{2x+y}=\dfrac{2}{\sqrt{y}}\\2+\dfrac{1}{2x+y}=\dfrac{2}{\sqrt{x}}\end{matrix}\right.\)

Lần lượt cộng vế với vế và trừ vế cho vế 2 pt ta được:

\(\left\{{}\begin{matrix}2=\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}\\\dfrac{1}{2x+y}=\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{y}}\end{matrix}\right.\)

Nhân vế với vế:

\(\dfrac{2}{2x+y}=\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}\right)\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{y}}\right)\)

\(\Leftrightarrow\dfrac{2}{2x+y}=\dfrac{1}{x}-\dfrac{1}{y}\)

\(\Leftrightarrow2x^2+xy-y^2=0\)

\(\Leftrightarrow\left(x+y\right)\left(2x-y\right)=0\)

\(\Leftrightarrow...\)

18.

Hình vẽ:

\(AH^2=\overrightarrow{AM}.\overrightarrow{AN}=AM.AN.cosMAN=AM.AN.cos0^o=AM.AN\)

\(\Rightarrow\dfrac{AH}{AM}=\dfrac{AN}{AH}\Rightarrow\Delta ANH\sim\Delta AHM\left(c-g-c\right)\)

\(\Rightarrow\widehat{ANH}=\widehat{AHM}=90^o\)

\(\Rightarrow\Delta ANH\) vuông tại \(N\)

\(\Rightarrow N\) thuộc đường tròn đường kính \(AH\)

19.

a, Ta có \(\overrightarrow{OM}.\overrightarrow{OA}=OM.OA.cos\widehat{MOA_i}=R^2.\widehat{MOA_i}\left(i\in\left\{1;2;...;n\right\}\right)\)

\(\Rightarrow cos\widehat{MOA_i}=\dfrac{1}{R^2}.\overrightarrow{OM}.\overrightarrow{OA}\)

Khi đó

\(cos\widehat{MOA_1}+cos\widehat{MOA_2}+...+cos\widehat{MOA_n}=\dfrac{1}{R^2}\overrightarrow{OM}.\left(\overrightarrow{OA_1}+\overrightarrow{OA_2}+...+\overrightarrow{OA_n}\right)=0\)

b, Theo định lí cosin:

\(cos\widehat{MOA_i}=\dfrac{OM^2+OA_i^2-MA_i^2}{2OM.OA}=\dfrac{2R^2-MA_i^2}{2R^2}=1-\dfrac{MA^2_i}{2R^2}\)

\(\Rightarrow cos\widehat{MOA_1}+cos\widehat{MOA_2}+...+cos\widehat{MOA_n}=n-\dfrac{MA_1^2+MA^2_2+...+MA_n^2}{2R^2}=0\)

\(\Rightarrow MA_1^2+MA^2_2+...+MA_n^2=2nR^2\) có giá trị không đổi

20.

\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+k\overrightarrow{BC}=\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\)

\(\Rightarrow AM^2=\left(1-k\right)^2.AB^2+k^2.AC^2+2\left(1-k\right).k.\overrightarrow{AB}.\overrightarrow{AC}\)

\(=\left(1-k\right)^2.c^2+k^2.b^2+2\left(1-k\right).k.AB.AC.cos\widehat{BAC}\)

\(=b^2k^2+c^2k^2-2c^2k+c^2+2\left(k-k^2\right)bc.\dfrac{b^2+c^2-a^2}{2bc}\)

\(=b^2k^2+c^2k^2-2c^2k+c^2+\left(k-k^2\right)\left(b^2+c^2-a^2\right)\)

\(=\left(k^2-k\right)a^2+kb^2+\left(k-1\right)^2\left(k^2+1\right)c^2\)