Ôn tập chương III

Gọi x là số sản phẩm sản xuất trong một ngày theo định mức.

Điều kiện x nguyên dương. Theo đề ta có chương trình:

\(\dfrac{360}{x}=\dfrac{360+\dfrac{360.5}{100}}{x+9}+1\)

⇔ x² + 27x – 3240 = 0

⇒ x₁= -72 (loại), x₂ = 45.

Thời gian giao hoàn thành kế hoạch là = 8 ngày

Nếu sản xuất theo thời gian đã định với năng suất mới thì số sản phẩm làm được là (45+9).8=432 sản phẩm.

Bấm MODE nhập 5 nhập 3

a, bấm 5 = -3 = -7 = ta được \(x_1=\dfrac{3+\sqrt{149}}{10};x_2=\dfrac{3-\sqrt{149}}{10}\)

Tương tự cho các câu còn lại

\(a,\Leftrightarrow\dfrac{\left(3x+4\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{x-2}{\left(x+2\right)\left(x-2\right)}=\dfrac{4+3x^2-12}{\left(x-2\right)\left(x+2\right)}\)

ĐKXĐ:\(x\ne2;x\ne-2\)

\(\Rightarrow3x^2+10x+8-x+2-4-3x^2+12=0\)

\(\Leftrightarrow\)\(9x+18=0\)

\(\Leftrightarrow x=-2\)(loại).
Vậy phương trình vô nghiệm.

b,ĐKXĐ:\(x\ne\dfrac{1}{2}\)

PT đã cho \(\Rightarrow6x^2-4x+6-6x^2+13x-5=0\)

\(\Leftrightarrow9x+1=0\)

\(\Leftrightarrow x=-\dfrac{1}{9}\left(tmđk\right)\)

c,\(ĐKXĐ:x\ge2\)

Bình phương 2 vế ta được:

\(x^2-4-x^2+2x-1=0\)

\(\Leftrightarrow2x-5=0\)

\(\Leftrightarrow x=\dfrac{5}{2}\left(tmđk\right)\)

Gọi p/s thứ nhất là \(\dfrac{1}{x}\), p/s thứ 2 là \(\dfrac{1}{y}\), p/s thứ 3 là \(\dfrac{1}{z}\)

Theo đề bài ta có : \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1\) (1)

và \(\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{z}\); \(\dfrac{1}{x}+\dfrac{1}{y}=5\cdot\left(\dfrac{1}{z}\right)\).

Thay biểu thức \(\dfrac{1}{x}+\dfrac{1}{y}=5\cdot\left(\dfrac{1}{z}\right)\) trên vào (1) ta được :

\(5\cdot\left(\dfrac{1}{z}\right)+\dfrac{1}{z}=1\Rightarrow z=6\) Vậy phân số thứ ba là \(\dfrac{1}{6}\).

Ta có : \(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{6}\\\dfrac{1}{x}+\dfrac{1}{y}=5\cdot\dfrac{1}{6}\end{matrix}\right.\left(Đề-bài\right)\)

Bài toán tổng hiệu \(\dfrac{1}{x}\) là số lớn, \(\dfrac{1}{y}\) là số bé (do \(\dfrac{1}{x}-\dfrac{1}{y}\) ra số dương).

Vậy \(\dfrac{1}{x}=\dfrac{\left(\dfrac{1}{6}+5\cdot\dfrac{1}{6}\right)}{2}=\dfrac{1}{2}\); \(\dfrac{1}{y}=5\cdot\dfrac{1}{6}-\dfrac{1}{2}=\dfrac{1}{3}\)

Vậy phân số thứ nhất là \(\dfrac{1}{2}\), phân số thứ hai là \(\dfrac{1}{3}\), phân số thứ ba là \(\dfrac{1}{6}\).

Gọi x (giờ), y(giờ) là thời gian để công nhân thứ nhất, thứ hai làm riêng để sơn xong bức tường.

Ta có hệ phương trình:

\(\left\{{}\begin{matrix}\dfrac{7}{x}+\dfrac{4}{y}=\dfrac{5}{9}\\\dfrac{4}{x}+\dfrac{4}{y}=1-\dfrac{5}{9}-\dfrac{1}{18}=\dfrac{7}{18}\end{matrix}\right.\)

Giải hệ phương trình trên ta được: \(\dfrac{1}{x}=\dfrac{1}{18};\dfrac{1}{y}=\dfrac{1}{24}\)

Suy ra x = 18, y = 24.

Vậy mỗi người làm riêng, theo thứ tự, thời gian sơn xong bức tường là 18 giờ và 24 giờ.

mấy bài này là ở lớp 9 học kì 2 dùng cộng đại số là nhanh nhất hoặc bấm máy tính

Nếu mọi nghiệm của phương trình f(x) = g(x) đều là nghiệm của phương trình f₁(x) = g₁(x) thì phương trình

f₁(x) = g₁(x) được gọi là phương trình hệ quả của phương trình f(x) = g(x).

Ta viết f(x) = g(x) f₁(x) = g₁(x).

Ví dụ: Giải phương trình:

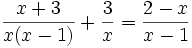(4)

Giải

Điều kiện của phương trình (4) là x ≠ 0 và x ≠ 1.

Nhân hai vế của phương trình (4) với x(x - 1) ta được phương trình hệ quả:

(4) x + 3 + 3(x - 1) = x(2 - x)

x² + 2x = 0

x(x + 2) = 0.

Phương trình cuối cùng có hai nghiệm là x = 0 và x = -2.

Ta thấy x = 0 không thỏa mãn điều kiện của phương trình (4), đó là nghiệm ngoại lai, nên bị loại. Còn lại x = -2 thỏa mãn điều kiện và thỏa mãn phương trình (4).

Vậy phương trình (4) có nghiệm duy nhất là x = -2.

Hai phương trình (cùng ẩn) được gọi là tương đương nếu chúng có cùng tập nghiệm.

Hai phương trình \(2x-5=0\)và \(3x-\dfrac{15}{2}=0\) tương đương với nhau vì cùng có nghiệm duy nhất \(x=\dfrac{5}{2}\)

a, ĐK x\(\ge5\) Đặt \(\sqrt{x-5}=y\Rightarrow x=y^2+5\)

Phương tình đã cho trở thành:\(y^2+5+y=y+6\)

\(\Leftrightarrow y^2-1=0\)

\(\Leftrightarrow y=-1;y=1\)

y=-1 loại vì \(\sqrt{x=5}\ge0\)

Ta có \(y=1\Rightarrow\sqrt{x-5}=1\Leftrightarrow x=6\)

b,làm tương tự câu a

c,ĐK:\(x\ge2\) Phương trình đã cho tương đương:\(\dfrac{x^2-8}{\sqrt{x-2}}=0\)

\(\Rightarrow\left[{}\begin{matrix}x_1=2\sqrt{2}\\x_2=-2\sqrt{2}\left(l\right)\end{matrix}\right.\)
Vậy phương trình có nghiệm \(x=2\sqrt{2}\).