Luyện tập về ba trường hợp bằng nhau của tam giác

a: Xét tứ giác ABNC có

M là trung điểm của AN và BC

=>ABNC là hình bình hành

=>AB=CN

b: AB+AC=CN+AC>NC=2AM

a: Xét ΔAEC và ΔABF có

AE=AB

góc EAC=góc BAF

AC=AF
=>ΔAEC=ΔABF

b: góc F+góc E=45+45=90 độ

=>góc FIE=90 độ

=>BF vuông góc CE

Đề bị thiếu điều kiện rồi nên không giải được em nhé!

 

`a,` Xét Tam giác `BAE` và Tam giác `BIE` có:

`BA = BI (g``t)`

\(\widehat{ABE} =\widehat{IAE}\) (tia phân giác \(\widehat{ABI}\))

`AE` chung

`=>` Tam giác `BAE =` Tam giác `BIE (c-g-c)`

`b,` vì Tam giác `BAE =` Tam giác `BIE` (a)

`=>` \(\widehat{BAE}=\widehat{BIE}=90^0\) (2 góc tương ứng)

`=> \(EI\perp BC\) 

`c,` Xét Tam giác `BAH và` Tam giác `BIH`

`BA=BI (g``t)`

\(\widehat{BAH}=\widehat{BIH}\) (tia phân giác \(\widehat{ABI}\))

`AH` chung

`=>` Tam giác `BAH =` Tam giác `BIH (c-g-c)`

`=>` \(\widehat{BHA}=\widehat{BHI}\) (2 góc tương ứng)

mà 2 góc này ở vị trí kề bù

`=>`\(\widehat{BHA}+\widehat{BHI}=180^0\)

`=>` \(\widehat{BHA}=\widehat{BHI} =\) \(\dfrac{180}{2}=90^0\)

`=>` \(BE\perp AI\) (đpcm)

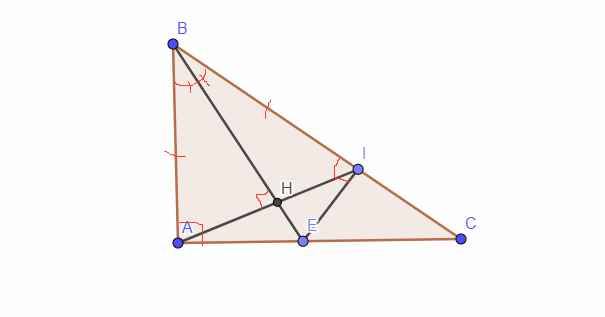
^{*Hình đây nha cậu, xl nãy làm bài mình quên gửi:').}

UKM THÌ CÓ BÀI TỰA VẬY BẠN SO ĐC CHỨ 

a) Xét AIM và BIC có:IA = IB (do I là trung điểm của AB);AIM BIC(hai góc đối đỉnh);IM = IC (giảthiết).Do đó AIM = BIC (c.g.c)Suy ra AM = BC (hai cạnh tương ứng) và MAI CBI(hai góc tương ứng)  Mà MAI, CBIlà hai góc ởvịtrí so le trong nên AM // BC.b) Xét ANE và CBE có:EA = EC (do E là trung điểm của AC);AEN CEB(hai góc đối đỉnh);EN= EB(giảthiết).Do đó ANE = CBE (c.g.c)Suy ra NAE BCE(hai góc tương ứng)Mà NAE, BCElà hai góc ởvịtrí so le trong nên AN// BC.c) Ta có AM // BC (theo câu a) và AN // BC (theo câu b)Do đó qua điểm A có hai đường thẳng song song với BC nên theo tiên đềEuclid, hai đường thẳng AM và AN trùng nhau hay ba điểm A, M, N thẳng hàng.Lại có ANE = CBE (theo câu b) nên AN = CB (hai cạnh tương ứng)Mặt khác AM = BC (theo câu a)Do đó AM = AN (cùng bằng BC)  Mà ba điểm A, M, N thẳng hàng nên A là trung điểm của MN.

a: Xét ΔAMB và ΔCMD có

MA=MC

góc AMB=góc CMD

MB=MD

Do đó: ΔAMB=ΔCMD

b: Xét tứ giác ABCD có

M là trung điểm chung của AC và BD

nên ABCD là hình bình hành

=>AB//CD và AB=CD

c: Xét tứ giác AKBC có

N là trung điểm chung của AB và KC

nên AKBC là hình bình hành

=>AK//BC

mà AD//BC

nên D,A,K thẳng hàng

1: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung

AB=AD

Do đó: ΔCAB=ΔCAD

=>góc BCA=góc DCA

=>CA là phân giác của góc DCB

2: Xét ΔCHA vuông tại H và ΔCKA vuông tại K có

CA chung

góc HCA=góc KCA

Do đó: ΔCHA=ΔCKA

=>CK=CH

3: Xét ΔCDB có CH/CD=CK/CB

nên HK//DB

Xét ΔABH vuông tại H vàΔACH vuông tại H có

AB=AC

AH chung

DO đó: ΔABH=ΔACH

=>HB=HC và góc BAH=góc CAH

a: Ta có: ΔBCA cân tại A

mà AH là đường trung tuyến

nên AH vuông góc với BC

b: Xét ΔAHM vuông tại M và ΔAHN vuôngtại N có

AH chung

góc HAM=góc HAN

Do đó: ΔAHM=ΔAHN

=>AM=AN

c: Xét ΔABC có AM/AB=AN/AC

nên MN//BC