giải pt sau
a)\(\sqrt[3]{2x+1}=3\)
b)\(\sqrt[3]{5+x}-x=5\)
c)\(\sqrt[3]{2-3x}=-2\)
d)\(\sqrt[3]{x-1}+1=x\)
Helpppp pls
Bài 9: Căn bậc ba
a: =>2x+1=27
=>2x=26
=>x=13
b: =>\(\sqrt[3]{x+5}=x+5\)
=>x+5=(x+5)^3
=>(x+5)(x+4)(x+6)=0
=>x=-5;x=-4;x=-6
c: =>2-3x=-8
=>3x=10
=>x=10/3
d: =>\(\sqrt[3]{x-1}=x-1\)
=>(x-1)^3=(x-1)
=>x(x-1)(x-2)=0
=>x=0;x=1;x=2
Đúng 0
Bình luận (0)
bài 6b,7a,7b 
6B.
a)\(\sqrt[3]{4-2x}\ge4\Leftrightarrow4-2x\ge64\)
\(\Leftrightarrow2x\le-60\Leftrightarrow x\le-30\)
Vậy...
b) \(\sqrt[3]{-x^3-3x^2+6x-10}< -x-1\)
\(\Leftrightarrow-x^3-3x^2+6x-10< -\left(x+1\right)^3\)
\(\Leftrightarrow-x^3-3x^2+6x-10< -x^3-3x^2-3x-1\)
\(\Leftrightarrow9x< 9\Leftrightarrow x< 1\)
Vậy...
7A.
a) \(\sqrt[3]{2x+1}=3\Leftrightarrow2x+1=27\Leftrightarrow x=13\)
Vậy...
b) \(\sqrt[3]{5+x}-x=5\)
\(\Leftrightarrow5+x=\left(5+x\right)^3\) \(\Leftrightarrow\left[{}\begin{matrix}5+x=0\\\left(5+x\right)^2=1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-4\\x=-6\end{matrix}\right.\)
Vậy...
7B.
a) PT \(\Leftrightarrow2-3x=-8\Leftrightarrow x=\dfrac{10}{3}\)
b) PT \(\Leftrightarrow x-1=\left(x-1\right)^3\)
\(\Leftrightarrow\left(x-1\right)\left[1-\left(x-1\right)^2\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^2=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\\x=2\end{matrix}\right.\)
Vậy...
Đúng 1
Bình luận (0)
\(\sqrt[3]{2x+1}>-5\)
\(\sqrt[3]{2x+1}>-5\)
\(\Leftrightarrow2x+1>\left(-5\right)^3\)
\(\Leftrightarrow2x+1>-125\)
\(\Leftrightarrow2x>-125-1\)
\(\Leftrightarrow2x>-126\)
\(\Leftrightarrow x>-\dfrac{126}{2}\)
\(\Leftrightarrow x>-63\)
Đúng 4
Bình luận (0)
3√2x+1>-5
\(\Leftrightarrow3\sqrt{2}\cdot x>-6\)
=>\(x>-\dfrac{6}{3\sqrt{2}}=-\sqrt{2}\)
Đúng 0
Bình luận (0)
Giải phương trình: \(\sqrt[3]{x}+\sqrt[3]{2x-3}=\sqrt[3]{12\left(x-1\right)}\)
\(\sqrt[3]{x}+\sqrt[3]{2x-3}=\sqrt[3]{12\left(x-1\right)}\left(1\right)\)
\(\left(1\right)\Leftrightarrow x+2x-3+3.\sqrt[3]{x\left(2x-3\right)}.\left(\sqrt[3]{x}+\sqrt[3]{2x-3}\right)=12x-12\)
\(\Rightarrow\sqrt[3]{12x\left(x-1\right)\left(2x-3\right)}=3x-3\)
\(\Leftrightarrow12x\left(x-1\right)\left(2x-3\right)=[3\left(x-1\right)]^3\)
\(\Leftrightarrow12x\left(2x^2-5x+3\right)=27\left(x^3-3x^2+3x-1\right)\)
\(\Leftrightarrow24x^3-60x^2+36x=27x^3-81x^2+81x-27\)
\(\Leftrightarrow3x^3-21x^2+45x-27=0\)
\(\Leftrightarrow3\left(x-1\right)\left(x-3\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\). Thử lại ta thấy cả x=1;x=3 đều t/m bài toán
Vậy, pt có tập nghiệm là S={1;3}
Đúng 0
Bình luận (0)
Chứng minh rằng biểu thức \(\sqrt[3]{1+\sqrt{x}}+\sqrt[3]{1-\sqrt{x}}\le2\) với mọi số thực \(x\) (\(x\ge0\))
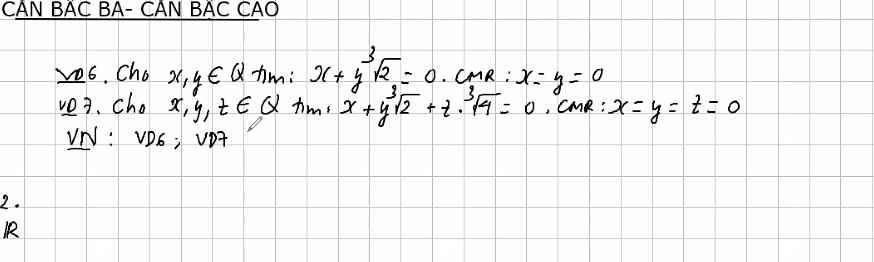 Nhờ mọi người giúp nình với ạ
Nhờ mọi người giúp nình với ạ
\(\sqrt[3]{x+1}+\sqrt[3]{x+8}=\sqrt[3]{2x+27}\)
\(\sqrt[3]{x+1}+\sqrt[3]{x+8}=\sqrt[3]{2x+27}\)
Cho phương trình x^3+(m-6)x-m+5=0
Tìm m để pt có 2 nghiệm phân biệt trái dấu
Để pt có hai nghiệm phân biệt trái dấu thì -m+5<0
=>-m<-5
=>m>5
Đúng 0
Bình luận (0)






