a: \(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right)\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{x+2+\sqrt{x}\left(\sqrt{x}-1\right)-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}-1}\)
\(=\dfrac{-\sqrt{x}+1+x-\sqrt{x}}{\left(\sqrt{x}-1\right)^2}\cdot\dfrac{2}{x+\sqrt{x}+1}=\dfrac{2}{x+\sqrt{x}+1}\)
b: A=2/13
=>\(x+\sqrt{x}+1=13\)
=>\(x+\sqrt{x}-12=0\)
=>\(\left(\sqrt{x}+4\right)\left(\sqrt{x}-3\right)=0\)
=>\(\sqrt{x}-3=0\)
=>\(\sqrt{x}=3\)
=>x=9(nhận)
c: \(x+\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}+1\right)+1>=0\cdot1+1=1\forall x\) thỏa mãn ĐKXĐ
=>\(A=\dfrac{2}{x+\sqrt{x}+1}< =\dfrac{2}{1}=2\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x=0
a) A= \(\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
A= \(\left(\dfrac{x+2}{\sqrt{x^3}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{1}{\sqrt{x}-1}\right).\dfrac{2}{\sqrt{x}-1}\)
A= \(\left(\dfrac{x+2+x-\sqrt{x}-x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right).\dfrac{2}{\sqrt{x}-1}\)
A= \(\dfrac{2\left(x+3\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
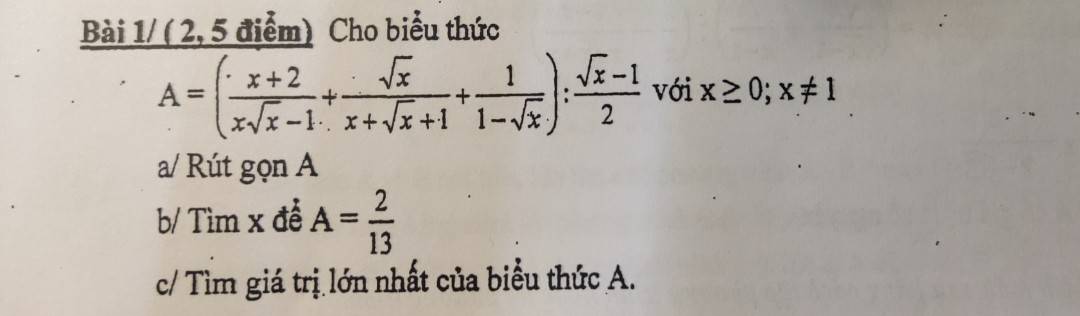



 giải giúp a b
giải giúp a b