Các bạn ơi cho mình hỏi là nếu hình đó mình vẽ thiếu 1 cái thì mình bị trừ bao nhiêu điểm ạ ( điểm tối đa của vẽ hình là 0,5)
Bài 6: Tam giác cân
Cái này tuỳ vào cách chấm em hi, có thể không trừ nhưng cũng có thể trừ sạch phần điểm hình
Đúng 0
Bình luận (0)
`1,`
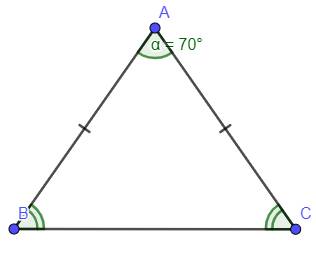
Có `Delta ABC` cân tại `A=>hat(B)=hat(C)=(180^0-hat(A))/2`
hay `hat(B)=hat(C)=(180^0-70^0)/2`
`=>hat(B)=hat(C)=55^0`
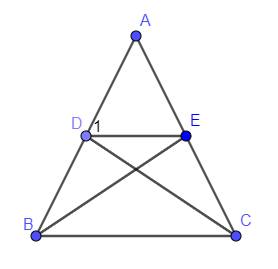
`2,`
`a)`
Có `Delta ABC` cân tại `A(GT)=>AB=AC`
mà `BD=CE(GT)`
nên `AB-BD=AC-CE`
hay `AD=AE`
`=>Delta ADE` cân tại `A(đpcm)`
`b)`
Có `Delta ABC` cân tại `A(GT)=>hat(ABC)=hat(ACB)`
hay `hat(DBC)=hat(ECB)`
Xét `Delta BDC` và `Delta CEB` có :
`{:(BC*chung),(hat(DBC)=hat(ECB)(cmt)),(BD=CE(GT)):}}`
`=>Delta BDC=Delta CEB(c.g.c)`
`=>CD=BE` ( 2 cạnh t/ứng )(đpcm)
`c)`
Có `Delta ABC` cân tại `A=>hat(ABC)=(180^0-hat(A))/2`
`Delta ADE` cân tại `A(cmt)=>hat(D_1)=(180^-hat(A))/2`
nên `hat(ABC)=hat(D_1)`
mà `2` góc này ở vị trí đvị
nên `DE////BC(đpcm)`
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A, kẻ BH,CK lần lượt vuông góc với AC,AB (H ϵ AC; K ϵ AB). Gọi O là giao điểm của BH và CK. Chứng minh:
a) BH=CK b) AO là phân giác của góc KAH
mình cần gấp các bn giúp mk với. mk cảm ơn nhiều!
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAKC
=>BH=CK
b: Xét ΔAKO vuông tại K và ΔAHO vuông tại H có
AO chung
AK=AH
=>ΔAKO=ΔAHO
=>góc KAO=góc HAO
=>AO là phân giác của góc KAH
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A biet góc A có số đo bằng 50 độ. tính só đo của góc còn lại của tam giác
Sửa đề: cân tại A
góc B=góc C=(180-50)/2=65 độ
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Từ A kẻ AH vuông góc với BC tại H (H€BC ). Viết giả thiết, kết luận , vẽ hình, chứng minh ∆AHB=∆AHC
GT ∆ABC cân tại A, AH BC
KL AHB = AHC
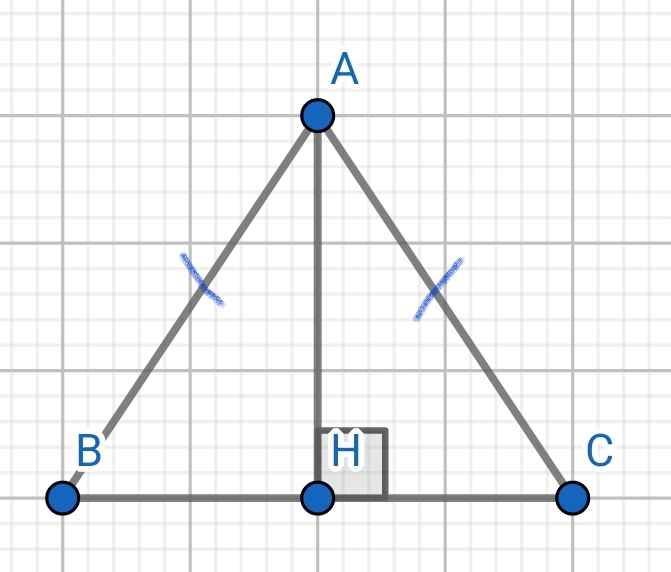
Xét hai tam giác vuông: ∆AHB và ∆AHC có:
AH chung
AB = AC (∆ABC cân tại A)
⇒ ∆AHB = ∆AHC (cạnh huyền - cạnh góc vuông)
Đúng 2
Bình luận (0)

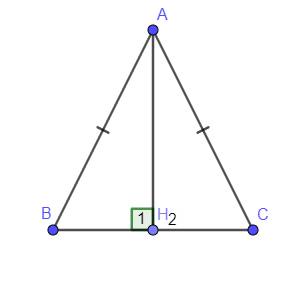
Có `AH⊥BC(GT)=>hat(H_1)=hat(H_2)(=90^0`
`Delta ABC` cân tại `A=>AB=AC`
Xét `Delta AHB` và `Delta AHC` có :
`{:(hat(H_1)=hat(H_2)(=90^0)),(AB=AC(cmt)),(AH-chung):}}`
`=>Delta AHB=Delta AHC(ch-cgv)(đpcm)`
Đúng 2
Bình luận (0)
Bài 4. Cho tam giác nhọn ABC, tia phân giác của góc B cắt cạnh AC tại D. Lấy điểm E trên cạnh BC sao cho AE BA. Chứng minh rằng:a) . b) Tam giác ADE cân. c) Gọi F là giao điểm của ED và BA. Chứng minh AE // FC.
Đọc tiếp
Bài 4. Cho tam giác nhọn ABC, tia phân giác của góc B cắt cạnh AC tại D. Lấy điểm E trên cạnh BC sao cho AE = BA. Chứng minh rằng:
a) ![]() .
.
b) Tam giác ADE cân.
c) Gọi F là giao điểm của ED và BA. Chứng minh AE // FC.
Cho tam giác ABC cân tại A.Tính số đo các góc B và C khi A=a⁰
`ΔABC` cân tại `A => hat{B} = hat{C} = (hat{B} + hat{C})/2`
Ta có: `hat{B} + hat{C} = 180^o - hat{A} = 180^o - a^o`
`=> hat{B} = hat{C} = (180^o - a^o)/2 = 90^o - (a^o)/2`
Đúng 2
Bình luận (0)
Cho △ABC cân tại A ( góc A<90°). Kẻ AH ⊥ BC tại H. a) △AHB =△AHC. Từ đó => BAH = CAH. b) trên tia AH lấy điểm K sao cho H là trung điểm AK
a: Xét ΔAHB vuôg tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔABH=ΔACH
=>góc BAH=góc CAH
b: Đề bài yêu cầu gì vậy bạn?
Đúng 0
Bình luận (1)
bạn vẽ giúp mình cái hình được không mình hơi băn khoang ở chỗ đó
Đúng 0
Bình luận (0)
cho tam giác ABC với AB nhỏ hơn AC , M là trung điểm của BC trên tia đối của tia MA lấy điểm E sao cho AM=EM . a, chứng minh tam giác AMB= tam giác EMC .b, từ A kẻ AH vuông góc với BC trên tia đối của tia HA lấy điểm D sao cho HA=HD chứng minh CE=BD .c, tam giác AMD là tam giác gì ? Vì sao ?
a: Xét ΔAMB và ΔEMC co
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔAMB=ΔEMC
b: Xet ΔBAD có
BH vừa là đường cao, vừa là trung tuyến
nên ΔBAD cân tại B
=>BD=BA=CE
c: Xét ΔAMD có
MH vừa là đường cao, vừa là trung tuyến
nên ΔAMD cân tại M
Đúng 3
Bình luận (0)
cho △MNP cân tại M. Từ M kẻ MH ⊥ NP tại H. Trên MH lấy điểm I tùy ý (I khác M và H)
a) PH = NH
b) NI = PI
a: ΔMNP cân tại M
mà MH là đường cao
nên H là trung điểm của NP
b: ΔMNP cân tại M
mà MH là đường cao
nên MH là trung trực của NP
=>I nằm trên trung trực của NP
=>IN=IP
Đúng 1
Bình luận (1)








