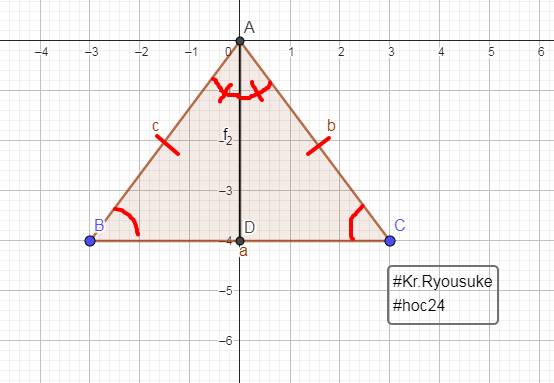
cho tam giác ABC cân tại A, tia phân giác của góc B cắt AC tại F, tia phân giác góc C cắt AB tại E. Chứng minh: a) góc ABF = góc ACE b) tam giác AEF cân c) gọi I là giao điểm của BF và CE.Chứng minh: tam giác IBC và IEF cân
help câu này với ạ
Bài 6: Tam giác cân
a: góc ABF=1/2*góc ABC
góc ACE=1/2*góc ACB
mà góc ACB=góc ABC
nên góc ABF=góc ACE
b: Xét ΔABF và ΔACE có
góc ABF=góc ACE
AB=AC
góc BAF chung
=>ΔABF=ΔACE
=>AF=AE
=>ΔAFE cân tại A
c: Xét ΔIBC có góc IBC=góc ICB
nên ΔIBC cân tại I
=>IB=IC
IB+IF=BF
IC+IE=CE
mà BF=CE và IB=IC
nên IF=IE
=>ΔIFE cân tại I
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A, tia phân giác của góc B cắt AC tại F, tia phân giác góc C cắt AB tại E. Chứng minh: a) góc ABF = góc ACE b) tam giác AEF cân c) gọi I là giao điểm của BF và CE.Chứng minh: tam giác IBC và IEF cân
Giúp mình với ạ
a: góc ABF=1/2*góc ABC
góc ACE=1/2*góc ACB
mà góc ACB=góc ABC
nên góc ABF=góc ACE
b: Xét ΔABF và ΔACE có
góc ABF=góc ACE
AB=AC
góc BAF chung
=>ΔABF=ΔACE
=>AF=AE
=>ΔAFE cân tại A
c: Xét ΔIBC có góc IBC=góc ICB
nên ΔIBC cân tại I
=>IB=IC
IB+IF=BF
IC+IE=CE
mà BF=CE và IB=IC
nên IF=IE
=>ΔIFE cân tại I
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, tia phân giác góc B , góc C cắt nhau tại I. Kẻ IH vuông góc AC.
a)Chứng minh: tam giác AIC cân
b)Chứng minh: AH=IK
kẻ hình hộ mình vs nhé
Và chứng minh hộ mình vs nhé 🫰🫰🫰🫰
sossssssCho tam giác ABC cân tại A , các đường phân giác BE,CF .CM rằng BEFC là hình thang cân có đáy nhỏ bằng cạnh bên
mn giúp mình nha mình đang cần gấp í ( mn nhớ vẽ hình nha )
Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc BAE chung
=>ΔABE=ΔACF
=>AE=AF
Xét ΔABC có AF/AB=AE/AC
nên FE//BC
Xét tứ giác BFEC có
FE//BC
góc FBC=góc ECB
=>BFEC là hình thang cân
Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A, góc A=70 độ, đường phân giác AD cắt BC ở D.Tính CAD
Vì \(\text{AD}\) là đường phân giác của $\widehat {BAC}$
`->` $\widehat {BAD} = \widehat {CAD}$
Mà $\widehat {A}=70^0$
`->`$\widehat {BAD} = \widehat {CAD}$ `= 70/2=35^0`
Vậy, số đo góc của $\widehat {CAD}$ là `35^0`
Đúng 0
Bình luận (0)
cho tam giác MNP cân tại M có MP = 6cm , MN = 10cm. Vẽ trung tuyến MH.Chứng minh MH là trung trực của NP.
a, chứng minh MH là trung trực của NP
b, điểm cách đều 3 đỉnh của tam giác có nằm trên MH không?
c, Vì sao góc MPH nhỏ hơn góc HMP
giải giúp mình vs ạ!
a: ΔMNP cân tại M
mà MH là đường trung tuyến
nên MH là trung trực của NP
b: MH là trung trực của NP
nên chắc chắn điểm cách đều 3 đỉnh nằm trên MH
c: HP=MN/2=5cm
=>MH=căn 6^2-5^2=căn 11(cm)
Vì MH<HP
nên góc MPH<góc HMP
Đúng 0
Bình luận (0)
Cho Tam giác ABC cân tại A,kẻ AH vuông góc với BC. A) CM: tam giác ABH=tam giác ÁCH B)gọi M là trung điểm,trên tia đối của tia MA lấy điểm N sao cho MA = MN . CM:tam giác AHM= tam giác NBM và NB vuông góc BC C) so sánh BAN và BNA Các bạn giúp mình nhé cảm ơn rất nhiều
a: Xet ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
=>ΔABH=ΔACH
b: Xet ΔAHM và ΔNBM có
MA=MN
góc AMH=góc NMB
HM=MB
=>ΔAMH=ΔNMB
=>góc NBM=90 độ
=>NB vuông góc BC
c: BN=AH
AH<AB
=>BN<BA
=>góc BAN<góc BNA
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên các cạnh AC, AB lần lượt lấy M, N sao cho AM = AN.
a) Chứng minh BN=CM
b) Gọi O là giao điểm của BM và CN. Chứng minh tam giác OBC cân.
a: AM+MC=AC
NA+NB=AB
mà AB=AC; AM=AN
nên MC=NB
b: Xét ΔNBC và ΔMCB có
NB=MC
góc NBC=góc MCB
BC chung
=>ΔNBC=ΔMCB
=>góc OBC=góc OCB
=>ΔOBC cân tại O
Đúng 1
Bình luận (0)
QH
1 tháng 4 2023 lúc 21:23
Xét ΔMBC và ΔNCB có
MB=NC
góc MBC=góc NCB
BC chung
=>ΔMBC=ΔNCB
=>góc OCB=góc OBC
=>OB=OC
Đúng 0
Bình luận (0)
Cho Tam giác bac cân tại a có b= 70 độ a,tính a,c b, kẻ AH vuông dóc với BC ( H thuộc BC) c, chứng minh AH là phân giác A Chứng minh Tam giác AHB bằng tam giác AHC
\(\text{#TNam}\)
`a,` Vì Tam giác `ABC` cân tại `A -> AB = AC,`\(\widehat{B}=\widehat{C}\)
Mà \(\widehat{B}=70^0 \)`->`\(\widehat{C}=70^0\)
Xét Tam giác `ABC:`
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\widehat{A}+70^0+70^0=180^0\)
\(\widehat{A}=180^0-70^0-70^0\)
`->`\(\widehat{A}=40^0\)
`b,` cm Tam giác `AHB =` Tam giác `AHC` `?`
Xét Tam giác `AHB` và Tam giác `AHC` có:
`AB = AC (CMT)`
\(\widehat{B}=\widehat{C}=70^0\)
\(\widehat{BHA}=\widehat{CHA}=90^0\)
`=> \text {Tam giác AHB = Tam giác AHC (ch-gn)}`
`c,` \(\text{Vì Tam giác AHB = Tam giác AHC (b)}\)
`->`\(\widehat{BAH}=\widehat{CAH} (\text {2 góc tương ứng)}\)
`-> \text {AH là tia phân giác của}`\(\widehat{BAC}\)
Đúng 1
Bình luận (0)