
Bài 4: Trường hợp bằng nhau thứ hai của tam giác cạnh - góc - cạnh (c.g.c)
Xét ΔAOD và ΔBOC ta có:
\(\widehat{ADO}=\widehat{BCO}\left(gt\right)\)
\(OD=OC\left(gt\right)\)
\(\widehat{AOD}=\widehat{BOC}\) (hai góc đổi đỉnh)
⇒ ΔAOD = ΔBOC (g-c-g)
Đúng 1
Bình luận (0)
Cho tam giác ABC, trên các tia đối của tia AB,AC lấy D và E sao cho AD=AB,AE=AC. Chứng minh DE song song BC
Xét tứ giác BCDE có
A là trung điểm chung của BD và CE
=>BCDE là hình bình hành
=>DE//BC
Đúng 0
Bình luận (0)
Cho góc nhọn xOoy có tia Oz là tia phân giác. Qua điểm a thuộc tia Ox vẽ đường thẳng song song với Ox cắt Oy tại B a) Chứng minh ∆OAM=∆MOB b) Từ M kẻ MH vuông góc Oy. Chứng minh ∆MHO = ∆MKO Hộ mik với ak, Mik cảm."_"^^
bài nà hơi kì nha . hình này vẽ bằng niềm tin à
Đúng 0
Bình luận (1)
Tam giác ABC vuông tại A . Phân giác B cắt AC tại D . Trên BC lấy M sao cho BA = BM
a) Chứng minh MD vuông góc BC
b) Chứng minh AM vuông góc BD
c)AMD = 36 độ
Tính B , C tam giác ABC
a: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
=>góc BMD=90 độ
=>DM vuông góc BC
b: BA=BM
DA=DM
=>BD là trung trực của AM
=>BD vuông góc AM
c: góc AMD=36 độ
=>góc ADM=180-2*36=108 độ
=>góc ABC=72 độ
=>góc C=18 độ
Đúng 0
Bình luận (0)
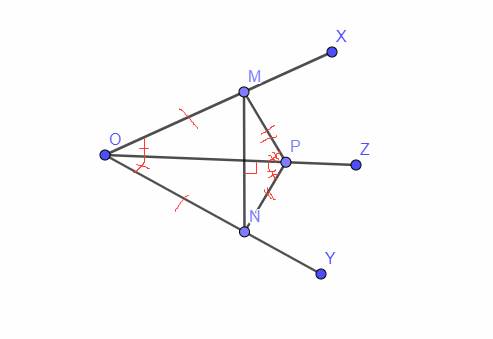
Cho tia xOy , Oz là tia phân giác của góc xOy . Điểm M nằm trên tia Ox, điểm N trên tia Oy sao cho OM= ON . a, chứng minh tam giác OMP= tam giác ONP. b, Gọi H là giao điểm của MN và OP, chứng minh MN vuông góc với OP
#\(N\)
`a,` Xét Tam giác `OMP` và Tam giác `ONP` có:
`OM = ON (g``t)`
\(\widehat{MOP}=\widehat{NOP}\) `(` tia phân giác \(\widehat{xOy}\) `)`
`OP` chung
`=>` Tam giác `OMP =` Tam giác `ONP (c-g-c)`
`b,` Vì Tam giác `OMP =` Tam giác `ONP (a)`
`=> MP = NP (` 2 cạnh tương ứng `)`
`=>`\(\widehat{MPH}=\widehat{NPH}\) `(` 2 góc tương ứng `)`
Xét Tam giác `MPH` và Tam giác `NPH` có:
`MP = NP (CMT)`
\(\widehat{MPH}=\widehat{NPH}(CMT)\)
`PH` chung
`=>` Tam giác `MPH = `Tam giác `NPH (c-g-c)`
`=>`\(\widehat{MHP}=\widehat{NHP}\) `(` 2 góc tương ứng `)`
Mà `2` góc này ở vị trí kề bù
`=>`\(\widehat{MHP}+\widehat{NHP}=180^0\)
`=>` \(\widehat{MHP}=\widehat{NHP}=\)\(\dfrac{180}{2}=90^0\)
`=>`\(MN\perp OP\left(đpcm\right)\)
Đúng 1
Bình luận (0)
tam giác ABC, kẻ Ax//BC (Ax và C nằm khác phía đối với AB. Trên Ax lấy M sao cho AM=BC. Chứng minh a; MB=AC b; MB=AC
Xét tứ giác AMBC có
AM//BC
AM=BC
Do đó: AMBC là hình bình hành
=>MB=AC
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Kẻ tia phân giác của ABC cắt cạnh AC tại M. Trên cạnh BC lấy điểm N sao cho BN = BA.
1) Chứng minh: tam giác BAM = tam giác BNM.
2) Gọi I là giao của BM và AN. Chứng minh I là trung điểm của đoạn thẳng AN.
3) Trên tia đối của tia AB lấy điểm K sao cho AK = NC. Chứng minh ABC = NMC và K, M, N là ba điểm thẳng hàng.
Cíu với ngày kia thi r:(
1: Xét ΔBAM và ΔBNM có
BA=BN
góc ABM=goc NBM
BM chung
Do đó: ΔBAM=ΔBNM
2: ΔBAM=ΔBNM
=>MA=MN
mà BA=BN
nên BM là trung trực của AN
=>I là trung điểm của AN
3: góc ABC+góc C=90 độ
góc NMC+góc C=90 độ
=>góc ABC=góc NMC
Đúng 0
Bình luận (0)
1,xét tgBAM và tgBNM có:
BA=BN gt
ABM=NBM gt
Bm chung
vậy 2 tg bằng nhau (c-g-c)
2,xét tgBAI và tgBNI có
BA=BN
ABI=NBI
BI chung
vậy 2tg bằng nhau(c-g-c)
Vì tg BAI=tgBNI (cmt)
suy ra IA=IN (tương ứng)
nên I là trung điểm của AN
Đúng 0
Bình luận (0)
Cho góc nhọn xoy .trên tia đối của tia ox lấy điểm a,trên tia đối của tia oy lấy điểm b sao cho oa=ob.trên tia ax lấy điểm c,trên tia by lấy điểm d sao cho ac=bd và ob<od,oa<oc
a) Chứng minh ad=bc
b) gọi e là giao điểm của advà bc.chứng minh tam giác eac= tam giác ebd
a: Xét ΔOAD và ΔOBC có
OA=OB
góc O chung
OD=OC
Do đó: ΔOAD=ΔOBC
=>AD=BC
b: Xét ΔEAC và ΔEBD có
góc EAC=góc EBD
AC=BD
góc ECA=góc EDB
Do đó: ΔEAC=ΔEBD
Đúng 1
Bình luận (0)
Cho tam giác ABC ( AB < AC ). Trên tia AB lấy điểm D sao cho AD = AD. Trên cạnh AC lấy điểm M sao cho AM = AB. Nối DM cắt BC tại I.
a) C/m rằng : Tam giác AMD = Tam giác ABC
Xét ΔAMD và ΔABC có
AM=AB
góc A chung
AD=AC
Do đó; ΔAMD=ΔABC
Đúng 1
Bình luận (0)



