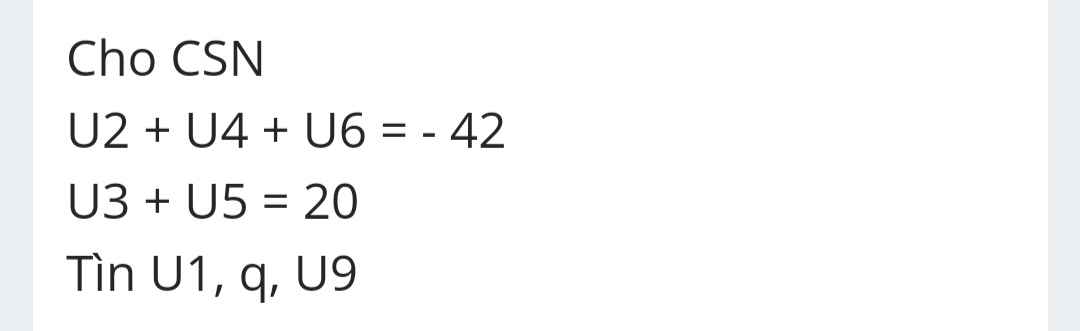Bài 4: Cấp số nhân
\(\left\{{}\begin{matrix}u_1q=6\\u_1+u_1q+u_1q^2=43\end{matrix}\right.\)
\(\Rightarrow\dfrac{1+q+q^2}{q}=\dfrac{43}{6}\)
\(\Rightarrow6q^2-37q+6=0\)
\(\Rightarrow\left[{}\begin{matrix}q=6\Rightarrow u_1=1\\q=\dfrac{1}{6}\Rightarrow u_1=36\end{matrix}\right.\)
Đúng 0
Bình luận (0)
\(\left\{{}\begin{matrix}u_2+u_4+u_6=-42\\u_3+u_5=20\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u_1q+u_1q^3+u_1q^5=-42\\u_1q^2+u_1q^4=20\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}u_1q\left(1+q^2+q^4\right)=-42\\u_1q\left(q+q^3\right)=20\end{matrix}\right.\)
\(\Rightarrow\dfrac{1+q^2+q^4}{q+q^3}=\dfrac{-42}{20}\)
\(\Rightarrow10q^4+21q^3+10q^2+21q+10=0\)
\(\Rightarrow\left(2q^2+5q+2\right)\left(5q^2-2q+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}q=-2\Rightarrow u_1=1\\q=-\dfrac{1}{2}\Rightarrow u_1=64\end{matrix}\right.\)
Đúng 0
Bình luận (0)
\(\left\{{}\begin{matrix}u_2=6\\S_3=46\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1q=6\\u_1.\dfrac{1-q^3}{1-q}=46\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}u_1q=6\\u_1\left(q^2+q+1\right)=46\end{matrix}\right.\)
\(\Rightarrow\dfrac{q^2+q+1}{q}=\dfrac{23}{3}\)
\(\Rightarrow3q^2-20q+3=0\)
Kết quả của pt bậc 2 này xấu quá
Đúng 0
Bình luận (0)
ai giúp mình bài này với ạ, mình cảm ơn nhiều ![]()

c)\(\left\{{}\begin{matrix}u_1+u_3=3\\u_1^2+u_3^2=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_3=3\\\left(u_1+u_3\right)^2-2u_1u_3=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_3=3\\u_1u_3=2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}u_1=2\\u_3=1\end{matrix}\right.\\\left\{{}\begin{matrix}u_1=1\\u_3=2\end{matrix}\right.\end{matrix}\right.\)
Làm nốt (sử dụng công thức: \(u_n=u_1+\left(n-1\right)d\) để tìm được công sai
\(S_n=nu_1+\dfrac{n\left(n-1\right)}{2}d\) để tính tổng 15 số hạng đầu)
d)\(\left\{{}\begin{matrix}u_1+u_2+u_3=14\\u_1u_2u_3=64\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}u_2-d+u_2+u_2+d=14\\\left(u_2-d\right)u_2\left(u_2+d\right)=64\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_2=\dfrac{14}{3}\\\left(u_2^2-d^2\right)u_2=64\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\dfrac{14}{3}=u_2=u_1+d\\d=\dfrac{2\sqrt{889}}{21}\end{matrix}\right.\\\left\{{}\begin{matrix}\dfrac{14}{3}=u_1+d\\d=\dfrac{-2\sqrt{889}}{21}\end{matrix}\right.\end{matrix}\right.\)
(Làm nốt,số xấu quá)
e)\(\left\{{}\begin{matrix}u_1+u_2+u_3=7\\u_1^2+u_2^2+u_3^2=21\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_2+u_3=7\\u_1u_2u_3=\dfrac{21-\left(u_1+u_2+u_3\right)^2}{2}=-14\end{matrix}\right.\)
Làm như ý d)
Đúng 1
Bình luận (1)
giúp em với ạ
Đọc tiếp
giúp em với ạ
2.
\(u_2=u_1.q\)
\(\Leftrightarrow q=\dfrac{u_2}{u_1}=2\)
Đúng 0
Bình luận (0)
3.
\(\left\{{}\begin{matrix}u_2=3\\u_4=27\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1.q=3\\u_1.q^3=27\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1.q=3\\3q^2=27\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1.q=3\\q=\pm3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}u_1=1\\q=3\end{matrix}\right.\\\left\{{}\begin{matrix}u_1=-1\\q=-3\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}u_3=9\\u_3=-9\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Giải chi tiết bài này giúp em với ạ
Đọc tiếp
Giải chi tiết bài này giúp em với ạ
\(\left\{{}\begin{matrix}6u_2+u_5=1\\3u_3+2u_4=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6u_1.q+u_1.q^4=1\\3u_1.q^2+2u_1.q^3=-1\end{matrix}\right.\)
\(\Rightarrow u_1\left(6q+q^4+3q^2+2q^3\right)=0\)
\(\Leftrightarrow q^3+2q^2+3q+6=0\)
\(\Leftrightarrow\left(q+2\right)\left(q^2+3\right)=0\)
\(\Leftrightarrow q=-\text{}2\)
\(\Rightarrow u_1=\dfrac{1}{4}\)
\(\Rightarrow u_n=u_1.q^{n-1}=\dfrac{1}{4}.\left(-2\right)^{n-1}=\left(-2\right)^{n-3}\)
Đúng 1
Bình luận (0)
Bài này chỉ có thể dùng tính năng TABLE để kiểm tra chứ không thể giải (vì không ai có thể giải được pt bậc 7!)
\(S_8=u_1\dfrac{q^8-1}{q-1}=6560\Rightarrow\dfrac{q^8-1}{q-1}=3280\)
\(\Rightarrow q=3\)
Đúng 2
Bình luận (0)
Cho cấp số nhân \(\left(u_n\right)\) biết \(\left\{{}\begin{matrix}3\sqrt{3}u_2+u_5=0\\u^2_3+u^2_6=63\end{matrix}\right.\)
Tính tổng \(S=\left|u_1\right|+\left|u_2\right|+\left|u_3\right|+...+\left|u_{15}\right|\)
Chứng minh |q| < 1 thì CSN lùi vô hạn
Xem chi tiết
cho 4 dãy số sau \(u_n=4.\sqrt{5}^n\); \(v_n=12.\left(-3\right)^n\); \(w_n=3^n-4^n\); \(a_n=\left(-1\right)^{2n+1}.4^n\). hỏi trong dãy có bnhieu CSN, đó là các CSN nào?
Trong dãy có 3 cấp số nhân:
\(u_n=4\sqrt{5}.\sqrt{5}^{n-1}\) là CSN với \(\left\{{}\begin{matrix}u_1=4\sqrt{5}\\q=\sqrt{5}\end{matrix}\right.\)
\(v_n=-36.\left(-3\right)^{n-1}\) là CSN với \(\left\{{}\begin{matrix}u_1=-36\\q=-3\end{matrix}\right.\)
\(a_n=-4.4^{n-1}\) là CSN với \(\left\{{}\begin{matrix}u_1=-4\\q=4\end{matrix}\right.\)
Đúng 1
Bình luận (0)