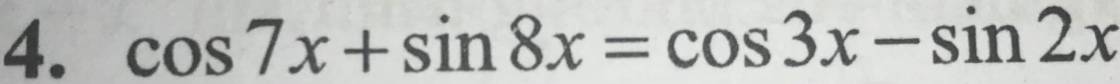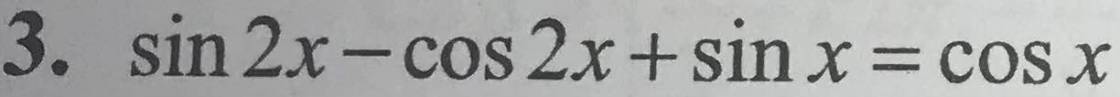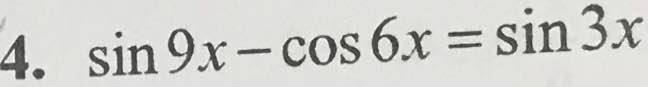
Bài 3: Một số phương trình lượng giác thường gặp

Chọn C

D

a: VP=sinx*sinpi/4+cosx*cospi/4

\(=sinx\cdot\dfrac{\sqrt{2}}{2}+cosx\cdot\dfrac{\sqrt{2}}{2}\)=VT

b: VP=cosx*cospi/6-sinx*sinpi/6

=cos(x+pi/6)

Trên \(\left[0;\dfrac{\pi}{6}\right]\) hàm \(cosx\) nghịch biến

\(\Rightarrow2.cos\left(\dfrac{\pi}{6}\right)+3\le y\le2.cos0+3\)

\(\Rightarrow3+\sqrt{3}\le y\le5\)

\(\Rightarrow M+m=8+\sqrt{3}\Rightarrow\left\{{}\begin{matrix}a=8\\b=1\end{matrix}\right.\)

1.

\(\Leftrightarrow sin5x=1-2cos^2x\)

\(\Leftrightarrow sin5x=-cos2x\)

\(\Leftrightarrow sin5x=sin\left(2x-\dfrac{\pi}{2}\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}5x=2x-\dfrac{\pi}{2}+k2\pi\\5x=\dfrac{3\pi}{2}-2x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\\x=\dfrac{3\pi}{14}+\dfrac{k2\pi}{7}\end{matrix}\right.\)

2.

\(\Leftrightarrow3sin^2x-7sinx.cosx+4cos^2x=0\)

Nhận thấy \(cosx=0\) ko phải nghiệm

Với \(cosx\ne0\) chia 2 vế cho \(cos^2x\)

\(\Rightarrow3tan^2x-7tanx+4=0\)

\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=\dfrac{4}{3}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=arctan\left(\dfrac{4}{3}\right)+k\pi\end{matrix}\right.\)

\(4cosx-3sin2x=0\)

\(\Leftrightarrow4cosx-6sinx.cosx=0\)

\(\Leftrightarrow2cosx\left(2-3sinx\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=\dfrac{2}{3}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=arcsin\left(\dfrac{2}{3}\right)+k2\pi\\x=\pi-arcsin\left(\dfrac{2}{3}\right)+k2\pi\end{matrix}\right.\)

`cos 7x+sin 8x=cos 3x-sin 2x`

`<=>sin 8x+sin 2x=cos 3x-cos 7x`

`<=>2sin 5x cos 2x=2sin 2x sin 5x`

`<=>sin 5x(cos 2x-sin 2x)=0`

`<=>sin 5x cos (2x+\pi/4)=0`

`<=>[(sin 5x=0),(cos (2x+\pi/4)=0):}`

`<=>[(5x=k\pi),(2x+\pi/4=\pi/2+k\pi):}`

`<=>[(x=k\pi/5),(x=\pi/8+k\pi/2):}`    `(k in ZZ)`

`sin 2x-cos 2x+sin x=cos x`

`<=>sin 2x-cos 2x=cos x-sin x`

`<=>-cos(2x+\pi/4)=cos(x+\pi/4)`

`<=>cos(2x+[5\pi]/4)=cos(x+\pi/4)`

`<=>[(2x+[5\pi]/4=x+\pi4+k2\pi),(2x+[5\pi]/4=-x-\pi/4+k2\pi):}`

`<=>[(x=-\pi+k2\pi),(x=[-13\pi]/36+k[2\pi]/3):}`

\(\Leftrightarrow sin9x-sin3x-cos6x=0\)

\(\Leftrightarrow2cos6x.cos3x-cos6x=0\)

\(\Leftrightarrow cos6x\left(2cos3x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos6x=0\\cos3x=\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow...\)

\(cos7x+cos3x+cos5x=0\)

\(\Leftrightarrow2cos5x.cos2x+cos5x=0\)

\(\Leftrightarrow cos5x\left(2cos2x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos5x=0\\cos2x=-\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow...\)