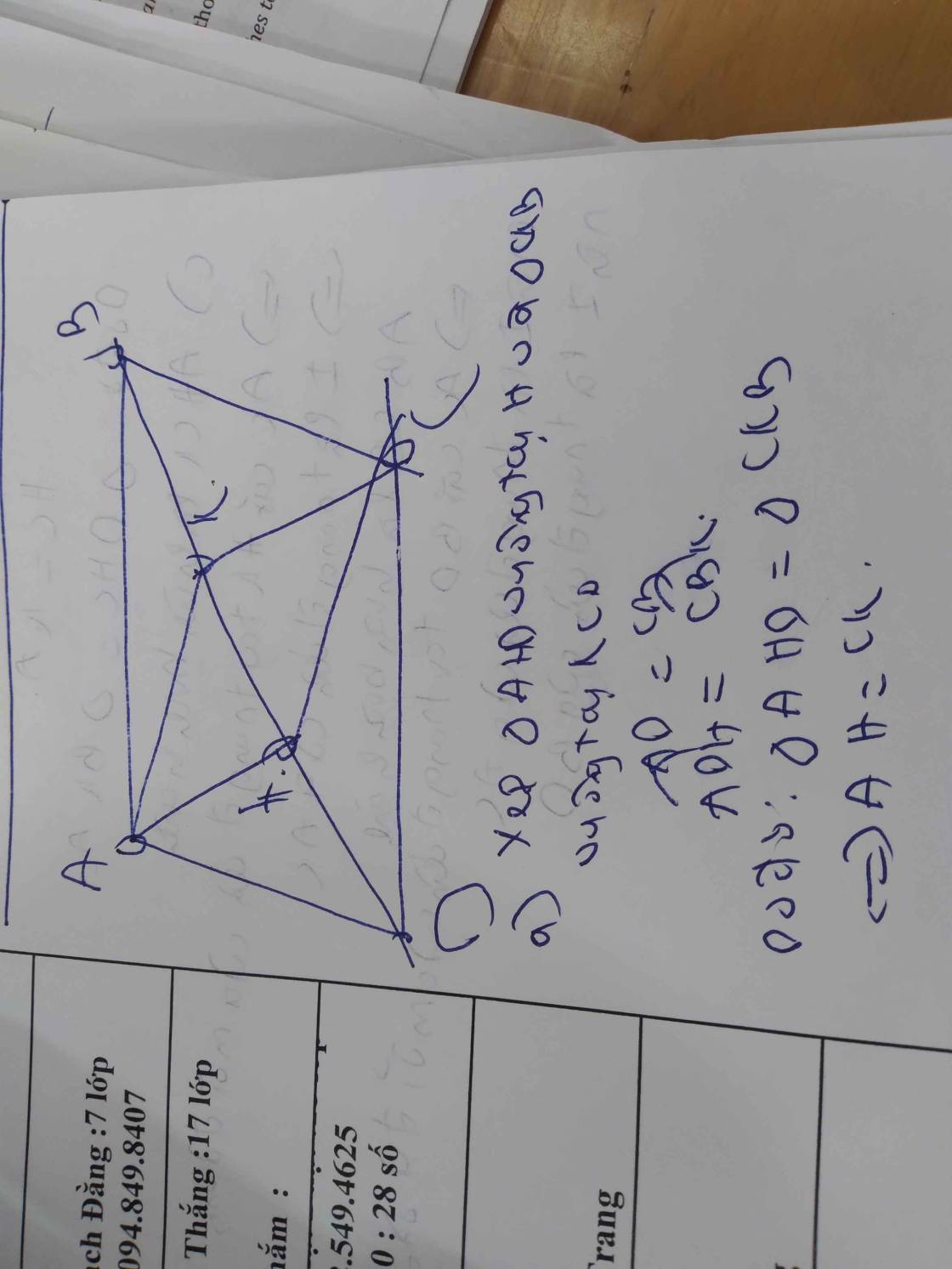
Chi tiết vẽ hình nữa ạ
Bài 3: Hình thang cân
Cho hình thang ABCD AB song song CD có góc C + góc D bằng 90 độ AB = 5 cm CD = 15 cm AD bằng 6 cm BC = 8 cm Tính diện tích hình thang
mn ơi cứu tôi với
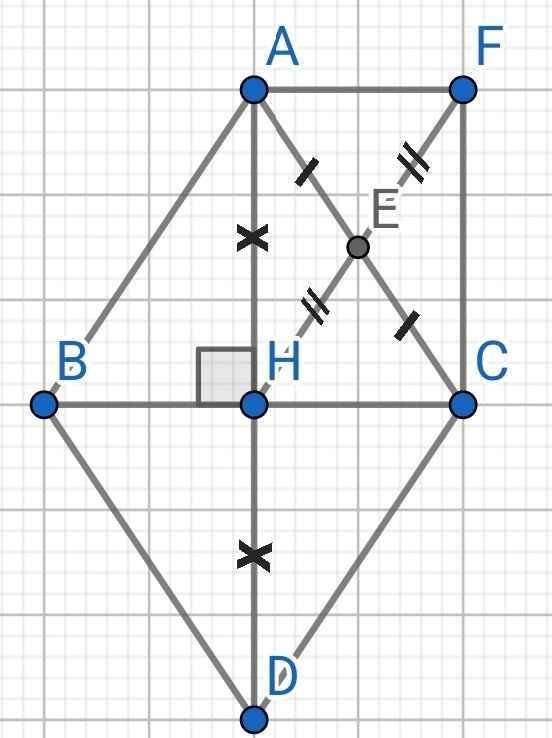 a) Do ∆ABC cân tại A có AH là đường cao
a) Do ∆ABC cân tại A có AH là đường cao
⇒ AH cũng là đường trung tuyến của ∆ABC
⇒ H là trung điểm của BC
Lại có HD = HA (gt)
⇒ H là trung điểm của AD
Ta có:
AH ⊥ BC
⇒ AD ⊥ BC
Xét tứ giác ABDC có:
H là trung điểm của BC (cmt)
H là trung điểm của AD (cmt)
⇒ ABDC là hình bình hành
Mà AD ⊥ BC (cmt)
⇒ ABDC là hình thoi
b) Do H là trung điểm của BC (cmt)
⇒ BH = BC : 2 = 6 : 2 = 3 (cm)
∆ABH vuông tại H (do AH ⊥ BC)
⇒ AB² = AH² + BH² (Pytago)
⇒ AH² = AB² - BH²
= 5² - 3²
= 16
⇒ AH = 4 (cm)
⇒ AD = AH = 4 (cm)
c) Tứ giác AHCF có:
E là trung điểm AC (gt)
E là trung điểm FH (gt)
⇒ AHCF là hình bình hành
Mà ∠AHC = 90⁰ (AH ⊥ BC)
⇒ AHCF là hình chữ nhật
⇒ AF ⊥ AH và FC ⊥ CH
d) Do ABDC là hình thoi (cmt)
⇒ ∠BAC = ∠BDC = 60⁰
Ta có:
∠BAC + ∠BDC + ∠ABD + ∠ACD = 360⁰ (tổng các góc của hình thoi ABDC)
⇒ ∠ABD + ∠ACD = 360⁰ - (∠BAC + ∠BDC)
= 360⁰ - (60⁰ + 60⁰)
= 360⁰ - 120⁰
= 240⁰
Mà ∠ABD = ∠ACD (hai góc đối của hình thoi ABDC)
⇒ ∠ABD = ∠ACD = 240⁰ : 2 = 120⁰
Vậy các góc của hình thoi ABDC lần lượt là:
∠BAC = ∠BDC = 60⁰
∠ABD = ∠ACD = 120⁰
Đúng 2
Bình luận (0)
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD (AB // CD) có E, F lần lượt là trung điểm
của các đáy AB, CD. Chứng minh EF vuông góc với AB và CD.

Do ABCD là hình thang cân
\(\Rightarrow AD=BC\) và \(\widehat{FDA}=\widehat{FCB}\)
Do F là trung điểm của CD (gt)
\(\Rightarrow FC=FD\)
Xét \(\Delta ADF\) và \(\Delta BCF\) có:
\(AD=BC\) (cmt)
\(\widehat{FDA}=\widehat{FCB}\) (cmt)
\(FD=FC\) (cmt)
\(\Rightarrow\Delta ADF=\Delta BCF\) (c-g-c)
\(\Rightarrow AF=BF\) (hai cạnh tương ứng)
\(\Delta FAB\) có:
\(AF=BF\) (cmt)
\(\Rightarrow\Delta FAB\) cân tại F
Lại có E là trung điểm của AB
\(\Rightarrow FE\) là đường trung tuyến của \(\Delta FAB\)
\(\Rightarrow FE\) cũng là đường cao của \(\Delta FAB\)
\(\Rightarrow FE\perp AB\)
Mà AB // CD (gt)
\(\Rightarrow FE\perp CD\)
Vậy EF vuông góc với AB và CD
Đúng 3
Bình luận (0)
Vẽ một hình thang cân ABCD có đáy AB song song CD, góc A bằng 60 độ cạnh AB bằng 6 cm, cạnh AD = BC = CB = 3 cm vẽ đường chéo BD .Hãy tính các góc của tam giác BCD?
Xét ΔBCD có:
\(BC=CD\left(gt\right)\)
\(\Rightarrow\text{Δ}BCD\) là tam giác cân tại C
Mà: ABCD là hình thang cân nên:
\(\widehat{BAD}=\widehat{ABC}=60^o\)
\(\widehat{ABC}+\widehat{DCB}=180^o\)
\(\Rightarrow\widehat{DCB}=180^o-60^o=120^o\)
ΔBCD lại là tam giác cân
\(\Rightarrow\widehat{DBC}=\widehat{CDB}=\dfrac{180^o-120^o}{2}=30^o\)
Đúng 0
Bình luận (0)
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác cân ABC (AB=AC). BD và CE là hai phân giác của gam giác:
a,CM:tam giác ABD=tam giác AEC.
b,CM: BCDE là hình thang cân.
GIÚP MÌNH VỚI PLSSSS
a: BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{1}{2}\cdot\widehat{ABC}\left(1\right)\)
CE là phân giác của góc ACB
=>\(\widehat{ACE}=\dfrac{1}{2}\cdot\widehat{ACB}\left(2\right)\)
ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
\(\widehat{ABD}=\widehat{ACE}\)
AB=AC
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE
b: ΔABD=ΔACE
=>AD=AE
Xét ΔABC có \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
nên DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
Hình thang BEDC có \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân
Đúng 0
Bình luận (0)
bài 1) Cho hình bình hành ABCD,vẽ AH vuông góc với DB tại H ,vẽ HC vuông góc với BD tại K(vẽ hình trước khi làm)a)cm:AHCK là hình bình hànhb)cm: Δ DHC Δ BKAc) Gọi I là trung điểm của HK ; cm:I là trung điểm DB theo tính chất của hình bình hành
Đọc tiếp
bài 1) Cho hình bình hành ABCD,vẽ AH vuông góc với DB tại H ,vẽ HC vuông góc với BD tại K(vẽ hình trước khi làm)a)cm:AHCK là hình bình hànhb)cm: Δ DHC= Δ BKAc) Gọi I là trung điểm của HK ; cm:I là trung điểm DB theo tính chất của hình bình hành