Bỏ câu a cũng được ạ, mình cần câu b với c :(
Cho hàm số y = (3m - 2) +9.
a) Tìm m để đồ thị của hàm số song song với đường thẳng y = 7x + 1
b) Tìm m để hàm số đi qua di qua điểm A(1;13)
c) Vẽ hàm số với m vừa tìm dược ở câu b.
Bỏ câu a cũng được ạ, mình cần câu b với c :(
Cho hàm số y = (3m - 2) +9.
a) Tìm m để đồ thị của hàm số song song với đường thẳng y = 7x + 1
b) Tìm m để hàm số đi qua di qua điểm A(1;13)
c) Vẽ hàm số với m vừa tìm dược ở câu b.
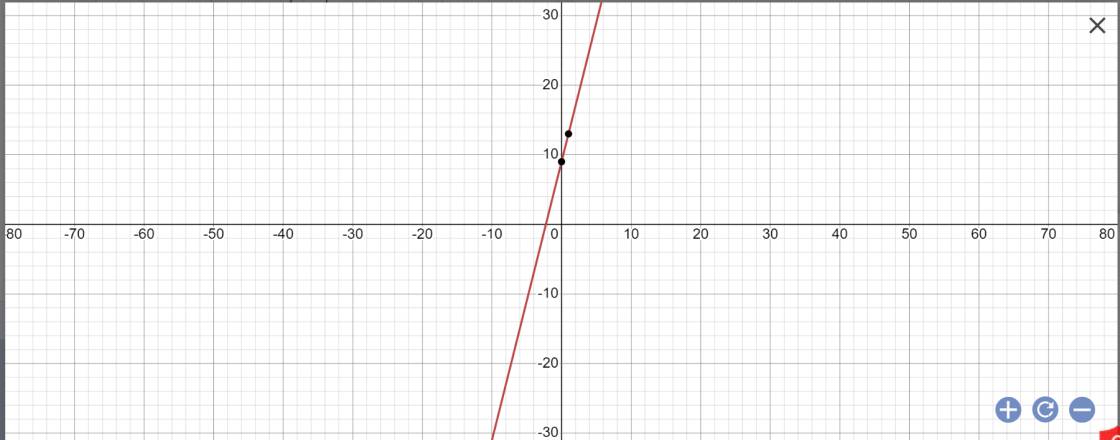
b: thay x=1 và y=13 vào (d), ta được:
3m-2+9=13
=>3m+7=13
=>m=2
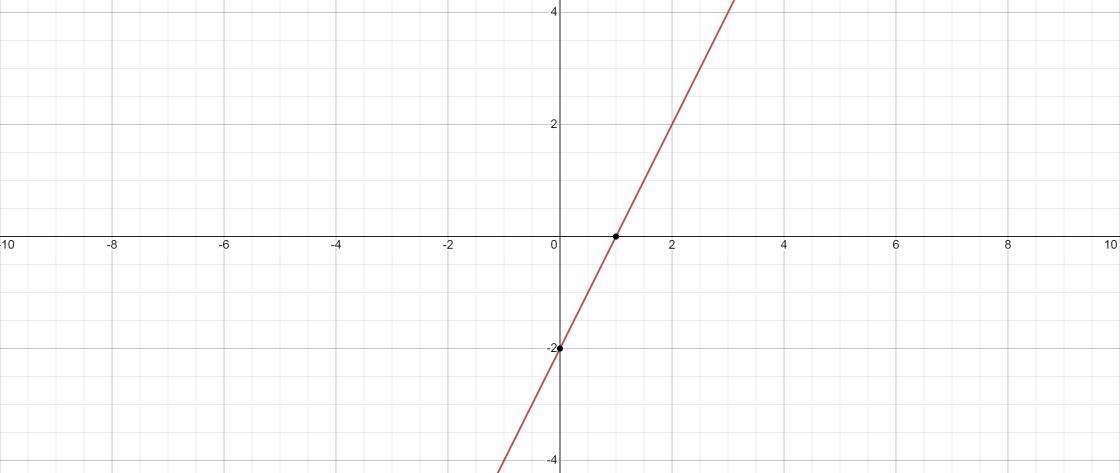
c: Khi m=2 thì (d): y=(3*2-2)x+9=4x+9
tìm K để biểu các điểm sau A(1;-1) , B(-5;-7) và C(2k-1;6) thẳng hằng
\(\overrightarrow{AB}=\left(-6;-6\right)\)
\(\overrightarrow{AC}=\left(2k-2;7\right)\)
Để A,B,C thẳng hàng thì \(\dfrac{-6}{2k-2}=\dfrac{-6}{7}\)
=>2k-2=7
=>k=9/2
cho đường thẳng (d): y = mx + 2 m Tìm m để khoảng cách từ gốc tọa độ đến đường thẳng
(d)là căn 2
Để tìm m để khoảng cách từ gốc tọa độ đến đường thẳng (d) là căn 2, ta sử dụng công thức tính khoảng cách từ một điểm đến một đường thẳng.
Đường thẳng (d) có phương trình y = mx + 2. Khoảng cách từ gốc tọa độ đến đường thẳng (d) được tính bằng công thức:
d = |Ax + By + C| / căn(A^2 + B^2)
Với A, B, C lần lượt là hệ số của x, y và số hạng tự do trong phương trình đường thẳng.
Trong trường hợp này, A = -m, B = 1, C = -2. Và khoảng cách từ gốc tọa độ đến đường thẳng (d) là căn 2.
Vậy ta có phương trình:
|0 - m*0 - 2| / căn((-m)^2 + 1^2) = căn 2
|0 - 2| / căn(m^2 + 1) = căn 2
| - 2| / căn(m^2 + 1) = căn 2
2 / căn(m^2 + 1) = căn 2
Bình phương cả hai vế của phương trình:
4 / (m^2 + 1) = 2
4 = 2(m^2 + 1)
4 = 2m^2 + 2
2m^2 = 2
m^2 = 1
m = ±1
Vậy, để khoảng cách từ gốc tọa độ đến đường thẳng (d) là căn 2, ta có hai giá trị của m: 1 và -1.
Cho hàm số y = mx + 2 tìm m để đồ thị hàm số cắt hai trục Ox Oy lần lượt tại A B sao cho chu vi tam giác OAB = 3 + căn 5
Để tìm m để đồ thị hàm số cắt hai trục Ox và Oy tại A và B sao cho chu vi tam giác OAB là 3 + căn 5, ta cần xác định tọa độ của A và B.
Điểm A nằm trên trục Ox, nên tọa độ của A là (x_A, 0). Thay vào phương trình hàm số y = mx + 2, ta có:
0 = mx_A + 2
=> mx_A = -2
=> x_A = -2/m
Điểm B nằm trên trục Oy, nên tọa độ của B là (0, y_B). Thay vào phương trình hàm số y = mx + 2, ta có:
y_B = m*0 + 2
=> y_B = 2
Chu vi tam giác OAB được tính bằng công thức chu vi tam giác:
chu_vi = AB + OA + OB
Với OA = x_A và OB = y_B, ta có:
chu_vi = AB + x_A + y_B
chu_vi = AB + (-2/m) + 2
chu_vi = AB - (2/m) + 2
Theo đề bài, chu vi tam giác OAB là 3 + căn 5, nên ta có:
3 + căn 5 = AB - (2/m) + 2
căn 5 = AB - (2/m) + 1
AB = căn 5 + (2/m) - 1
Ta đã có tọa độ của A và B, và chu vi tam giác OAB. Giờ ta sẽ tính độ dài AB:
AB = căn((x_A - 0)^2 + (y_B - 0)^2)
AB = căn((-2/m)^2 + 2^2)
AB = căn(4/m^2 + 4)
AB = căn(4(1/m^2 + 1))
AB = 2căn(1/m^2 + 1)
So sánh với công thức đã tính được trước đó:
AB = căn 5 + (2/m) - 1
Ta có:
2căn(1/m^2 + 1) = căn 5 + (2/m) - 1
Bình phương cả hai vế của phương trình:
4(1/m^2 + 1) = 5 + 4/m^2 + 1 - 4/m
4/m^2 + 4 = 6 + 4/m^2 - 4/m
8/m^2 = 2 - 4/m
Nhân cả hai vế của phương trình cho m^2:
8 = 2m^2 - 4
2m^2 = 12
m^2 = 6
m = ±√6
Vậy, để đồ thị hàm số cắt hai trục Ox và Oy tại A và B sao cho chu vi tam giác OAB là 3 + căn 5, ta có hai giá trị của m: √6 và -√6.
cho hàm số y=(m-2)x+1 tìm m đề hàm số nghịch biến trên R. Vẽ đồ thị của hàm số khi m=3
Giúp mình với
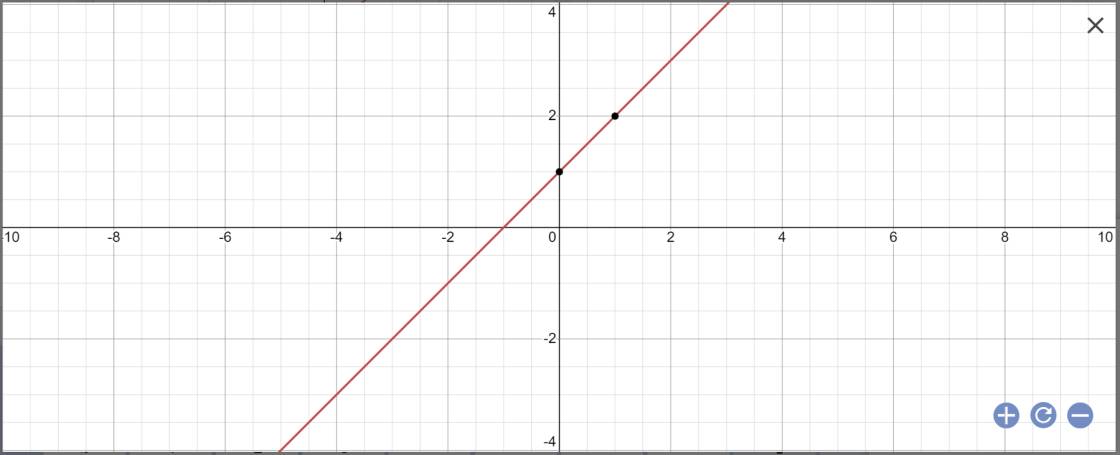
a: Để hàm số nghịch biến trên R thì m-2<0
=>m<2
b: Khi m=3 thì y=x+1
Cho các đường thẳng d1: y = x+ 1 và d2: y = x căn 3 -3
a) Vẽ d1 và d2 trên cùng một mặt phẳng tọa độ.
b) Gọi A và B lần lượt là giao điểm của d1, d2 với trục hoành và C là giao điểm của d1,d2. Tính số đo các góc của tam giác ABC
mình cần gấp, cảm ơnnhe
a: 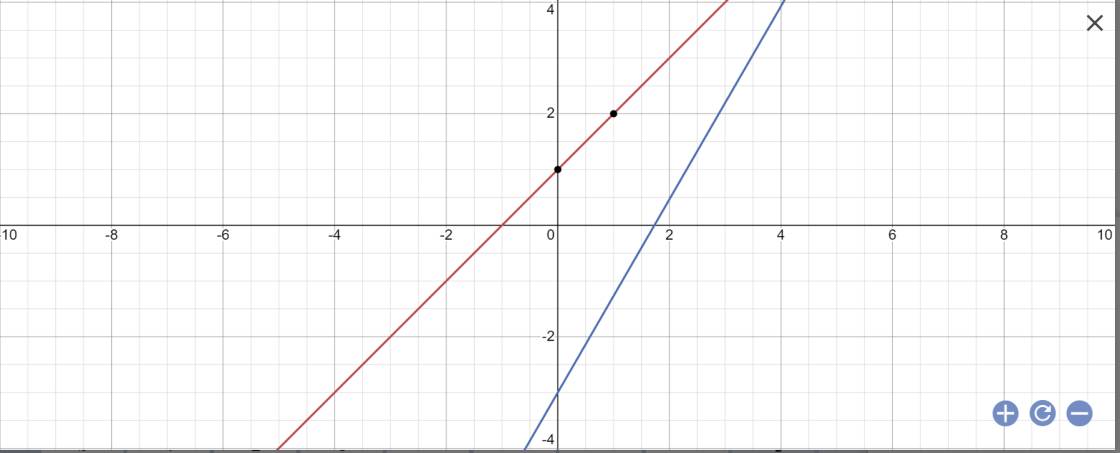
b: Tọa độ A là;
y=0 và x+1=0
=>x=-1 và y=0
Tọa độ B là:
y=0 và x*căn 3-3=0
=>x=căn 3 và y=0
Tọa độ C là:
x+1=xcăn 3-3 và y=x+1
=>\(x=\dfrac{-4}{-\sqrt{3}+1}=2+2\sqrt{3}\) và y=3+3căn 3
A(-1;0); B(căn 3;0); \(C\left(2+2\sqrt{3};3+3\sqrt{3}\right)\)
\(AC=\sqrt{\left(2+2\sqrt{3}+1\right)^2+\left(3\sqrt{3}\right)^2}\simeq8,29\)
\(AB=\sqrt{\left(\sqrt{3}+1\right)^2}\simeq2,73\)
\(BC=\sqrt{\left(2+2\sqrt{3}-\sqrt{3}\right)^2+\left(3+3\sqrt{3}\right)^2}\simeq9,0\left(cm\right)\)
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\simeq-\dfrac{245}{2487}\)
=>góc A=96 độ
\(cosB=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}=\dfrac{271}{675}\)
=>góc B=67 độ
=>góc C=17 độ
( d ) y = mx + 2
a . CM với mọi m thì đường thẳng ( d ) luôn cắt trục Oy tại điểm M ( 0 ; 2 )
Thay x=0 và y=2 vào (D), ta được:
m*0+2=2
=>2=2(luôn đúng)
Giả sử (d) cắt (Oy) tại M(0;2) , khi đó:
2=m.0+2 hay 2=2(luôn đúng)
=> ĐPCM
a: 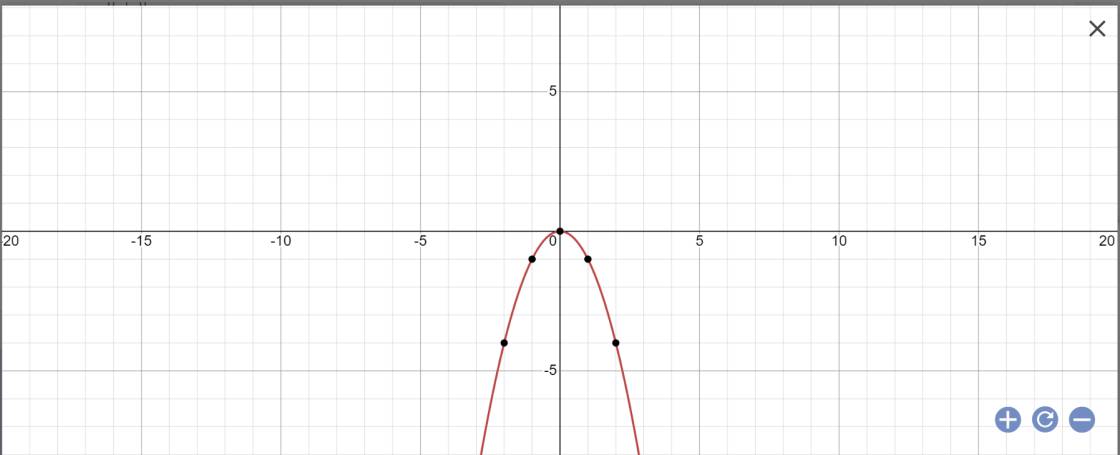
PTHĐGĐ là:
-x^2-2x+3=0
=>x^2+2x-3=0
=>(x+3)(x-1)=0
=>x=1 hoặc x=-3
=>y=-1 hoặc y=-9
Vẽ đồ thị của hai hàm số sau trên mặt phẳng tọa độ Oxy a) y = - 2x + 2
\(a,y=-2x+2\)
| \(x\) | \(0\) | \(1\) |
| \(y\) | \(-2\) | \(0\) |
Bài 3: cho phương trình bậc hai x^2-(m+1)x+m=0
a) chứng tỏ rằng phương trình luôn có nghiệm với mọi m
b) tìm m để phương trình có hai nghiệm x1, x2 sao cho x1^2+x2^2+3x1x2=5
a: Δ=(m+1)^2-4m=(m-1)^2>=0
=>Phương trình luôn có nghiệm
b: x1^2+x2^2+3x1x2=5
=>(x1+x2)^2+x1x2=5
=>(m+1)^2+m=5
=>m^2+3m-4=0
=>(m+4)(m-1)=0
=>m=1 hoặc m=-4