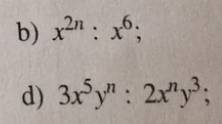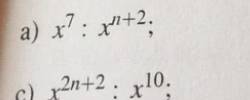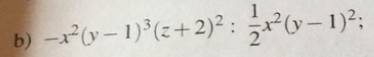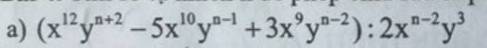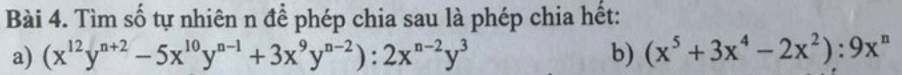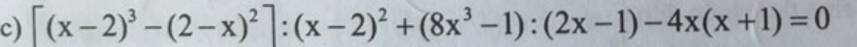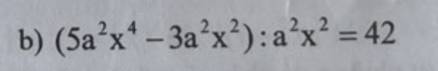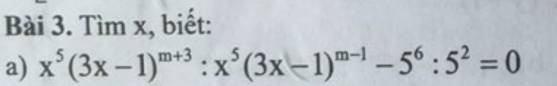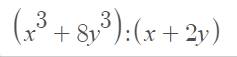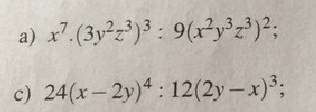
Bài 10: Chia đơn thức cho đơn thức

`(a):\  x^{7}.(3y^{2}z^{3})^{3}:9(x^{2}y^{3}z^{3})^{2}`

`=27x^{7}y^{6}z^{9}:9x^{4}y^{6}z^{6}`

`=3x^{3}z^{3}`

`(c)\  24(x-2y)^{4}:12(2y-x)^{3}`

`=24(2y-x)^{4}:12(2y-x)^{3}`

`=2(2y-x)`

`=4y-2x`

a: \(=\dfrac{x^7\cdot27y^6z^9}{9x^4y^6z^6}=3x^3z^3\)

c: \(=\dfrac{24\left(2y-x\right)^4}{12\left(2y-x\right)^3}=2\left(2y-x\right)\)

b: \(=x^{2n-6}\)

d: \(=\dfrac{3}{2}x^{5-n}\cdot y^{n-3}\)

a) \(x^7:x^{n+2}=x^{7-n-2}=x^{5-n}\)

b) \(x^{2n+2}:x^{10}=x^{2n+2-10}=x^{2n-8}\)

\(-x^2\left(y-1\right)^3\left(z+2\right)^2:\dfrac{1}{2}x^2\left(y-1\right)^2\)

\(=\dfrac{2.\left(-x^2\right)\left(y-1\right)^3\left(z+2\right)^2}{x^2\left(y-1\right)^2}=-2\left(y-1\right)\left(z+2\right)^2\)

\(=\dfrac{1}{2}x^{n+14}y^{n-1}-\dfrac{5}{2}x^{12-n}y^{n-4}+\dfrac{3}{2}x^{11-n}y^{n-5}\)

a, \(=\dfrac{1}{2}x^{14-n}y^{n-1}-\dfrac{5}{2}x^{12-n}y^{n-4}+\dfrac{3}{2}x^{11-n}y^{n-5}\)

b, \(=\dfrac{1}{9}x^{5-n}+\dfrac{1}{3}x^{4-n}-\dfrac{2}{9}x^{2-n}\)

\(\Leftrightarrow\left(x-2\right)-1+4x^2+2x+1-4x^2-4x=0\)

\(\Leftrightarrow-x=0\)

=>x=0

\(\Leftrightarrow x-2-1+\left(2x-1\right)\left(4x^2+4x+1\right):\left(2x-1\right)-4x^2-4x=0\)

\(\Leftrightarrow x-3+4x^2+4x+1-4x^2-4x\Leftrightarrow x-2=0\Leftrightarrow x=2\)

[(x - 2)³ - (2 - x)²] : (x - 2)² + (8x³ - 1) : (2x - 1) - 4x(x + 1) = 0

[(x - 2)³ + (x - 2)²] : (x - 2)² + [(2x - 1)(4x² + 2x + 1)] : (2x + 1) - 4x² - 4x = 0

x - 2 + 1 + 4x² + 2x + 1 - 4x² - 4x = 0

-x = 0

x = 0

Vậy x = 0

b, \(\dfrac{5a^2x^4}{a^2x^2}-\dfrac{3a^2x^2}{a^2x^2}=42\Rightarrow5x^2-3=42\Leftrightarrow x=\pm3\)

(5a²x⁴ - 3a²x²) : a²x² = 42

5x² - 3 = 42

5x² = 42 + 3

5x² = 45

x² = 45 ÷ 5

x² = 9

x = 3 hoặc x = -3

\(\left(3x-1\right)^4=5^4\Leftrightarrow\left[{}\begin{matrix}3x-1=5\\3x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\)

\(=x^2+4y^2\)

(x³ + 8y³) : (x + 2y)

= [(x + 2y)(x² + 2xy + 4y²)] : (x + 2y)

= x² + 2xy + 4y²