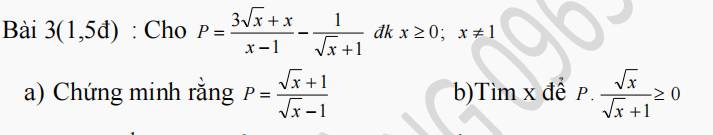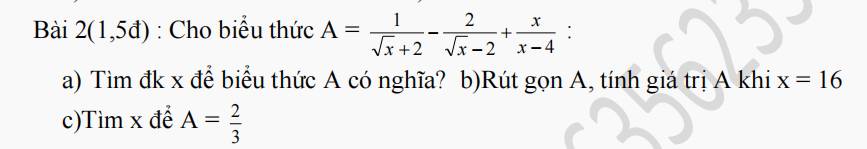Bài 1: Căn bậc hai
ĐKXĐ: -x^2+5x-4>=0 và 2x-7<>0
=>1<=x<=4 và x<>7/2
Đúng 0
Bình luận (0)
Tìm giá trị của x để biểu thức sau được xác định:
\(\sqrt{-x^2+5x-4}+\dfrac{1}{2x-7}\)
\(\sqrt{-x^2+5x-4}+\dfrac{1}{2x-7}\)
Được xác định khi:
\(\left\{{}\begin{matrix}-x^2+5x-4\ge0\\2x-7\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\left(x-4\right)\left(x-1\right)\ge0\\2x\ne7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}\left\{{}\begin{matrix}-\left(x-4\right)\ge0\\x-1\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}-\left(x-4\right)< 0\\x-1< 0\end{matrix}\right.\end{matrix}\right.\\x\ne\dfrac{7}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}\left\{{}\begin{matrix}-x\ge-4\\x\ge1\end{matrix}\right.\\\left\{{}\begin{matrix}-x< -4\\x< 1\end{matrix}\right.\end{matrix}\right.\\x\ne\dfrac{7}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left\{{}\begin{matrix}\left\{{}\begin{matrix}x\le4\\x\ge1\end{matrix}\right.\\\left\{{}\begin{matrix}x>4\\x< 1\end{matrix}\right.\end{matrix}\right.\\x\ne\dfrac{7}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}1\le x\le4\\x\ne\dfrac{7}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
\(\sqrt{7-\sqrt{24}}-\dfrac{\sqrt{50}-5}{\sqrt{10}-\sqrt{5}}+\sqrt{\left(11-\sqrt{120}\right)\left(11+2\sqrt{30}\right)^2}\)
Rút gọn giùm mình với ạ
\(\sqrt{7-\sqrt{24}}-\dfrac{\sqrt{50}-5}{\sqrt{10}-\sqrt{5}}+\sqrt{\left(11+\sqrt{120}\right)\left(11+2\sqrt{30}\right)^2}\)
\(=\sqrt{7-2\sqrt{6}}-\dfrac{5\left(\sqrt{2}-1\right)}{\sqrt{5}\left(\sqrt{2}-1\right)}+\left|11+2\sqrt{30}\right|\sqrt{11-2\sqrt{30}}\)
\(=\sqrt{1^2-2\sqrt{6}\cdot1+\left(\sqrt{6}\right)^2}-\dfrac{\sqrt{5}\cdot\sqrt{5}}{\sqrt{5}}+\left(11+2\sqrt{30}\right)\sqrt{\left(\sqrt{6}\right)^2-2\sqrt{5}\cdot\sqrt{6}+\left(\sqrt{5}\right)^2}\)
\(=\sqrt{\left(1-\sqrt{6}\right)^2}-\sqrt{5}+\left(11+2\sqrt{30}\right)\sqrt{\left(\sqrt{6}-\sqrt{5}\right)^2}\)
\(=\left|1-\sqrt{6}\right|-\sqrt{5}+\left(11+2\sqrt{30}\right)\left|\sqrt{6}-\sqrt{5}\right|\)
\(=-1+6-\sqrt{5}+\left(\sqrt{6}+\sqrt{5}\right)^2\left(\sqrt{6}-\sqrt{5}\right)\)
\(=\sqrt{6}-1-\sqrt{5}+\left[\left(\sqrt{6}\right)^2-\left(\sqrt{5}\right)^2\right]\left(\sqrt{6}+\sqrt{5}\right)\)
\(=\sqrt{6}-1-\sqrt{5}+\left(6-5\right)\left(\sqrt{6}+\sqrt{5}\right)\)
\(=\sqrt{6}-1-\sqrt{5}+\sqrt{6}+\sqrt{5}\)
\(=2\sqrt{6}-1\)
Đúng 1
Bình luận (0)
\(=\sqrt{6+1-2\sqrt{6}}-\dfrac{\sqrt{5}\left(\sqrt{10}-\sqrt{5}\right)}{\sqrt{10}-\sqrt{5}}+\sqrt{\left(11-\sqrt{120}\right)\left(11+\sqrt{120}\right)^2}\\ =\sqrt{\left(\sqrt{6}-\sqrt{1}\right)^2}-\sqrt{5}+\sqrt{\left(11^2-120\right)\left(11+2\sqrt{30}\right)}\\ =\sqrt{6}-\sqrt{1}-\sqrt{5}+\sqrt{1\left(6+5+2\sqrt{6\cdot5}\right)}\\ =\sqrt{6}-\sqrt{1}-\sqrt{5}+\sqrt{\left(\sqrt{6}+\sqrt{5}\right)^2}\\ =\sqrt{6}-\sqrt{1}-\sqrt{5}+\sqrt{6}+\sqrt{5}=2\sqrt{6}-\sqrt{1}\)
Đúng 0
Bình luận (0)
Cho biểu thức
A=a+b-√ab/a√a+b√b - √a-√b-1/a-b
( với a>0,b>0,a khác b)
a) Rút gọn b+a
b) Tính giá trị của A biết a-b=1
a: \(A=\dfrac{1}{\sqrt{a}+\sqrt{b}}-\dfrac{\sqrt{a}-\sqrt{b}-1}{a-b}\)
\(=\dfrac{\sqrt{a}-\sqrt{b}-\sqrt{a}+\sqrt{b}+1}{a-b}=\dfrac{1}{a-b}\)
b: Khi a-b=1 thì A=1/1=1
Đúng 0
Bình luận (0)
\(a,P=\dfrac{3\sqrt{x}+x}{x-1}-\dfrac{1}{\sqrt{x}+1}\left(dk:x\ge0,x\ne1\right)\)
\(=\dfrac{3\sqrt{x}+x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}+1}\\ =\dfrac{3\sqrt{x}+x-\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{2\sqrt{x}+x+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\left(dpcm\right)\)
\(b,P.\dfrac{\sqrt{x}}{\sqrt{x}+1}\ge0\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-1}.\dfrac{\sqrt{x}}{\sqrt{x}+1}\ge0\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-1}\ge0\\ \Leftrightarrow x\ge0\)
Vậy \(x\ge0\) thì thỏa mãn đề bài.
Đúng 0
Bình luận (0)
a: \(P=\dfrac{\sqrt{x}+5-3}{\sqrt{x}+5}=1-\dfrac{3}{\sqrt{x}+5}\)
căn x+5>=5
=>3/(căn x+5)<=3/5
=>-3/(căn x+5)>=-3/5
=>P>=2/5
Dấu = xảy ra khi x=0
b: \(Q=\dfrac{3\sqrt{x}+6-5}{\sqrt{x}+2}=3-\dfrac{5}{\sqrt{x}+2}\)
căn x+2>=2
=>5/căn x+2<=5/2
=>-5/căn x+2>=-5/2
=>Q>=1/2
Dấu = xảy ra khi x=0
c: \(E=\dfrac{\sqrt{x}+1+5}{\sqrt{x}+1}=1+\dfrac{5}{\sqrt{x}+1}< =1+\dfrac{5}{1}=6\)
Dấu = xảy ra khi x=0
d: \(D=\dfrac{2\sqrt{x}+4+3}{\sqrt{x}+2}=2+\dfrac{3}{\sqrt{x}+2}>=2+\dfrac{3}{2}=\dfrac{7}{2}\)
Dấu = xảy ra khi x=0
Đúng 0
Bình luận (0)
\(a,\) A có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}x\ge0\\x\ne4\end{matrix}\right.\)
\(b,A=\dfrac{1}{\sqrt{x}+2}-\dfrac{2}{\sqrt{x}-2}+\dfrac{x}{x-4}\\ =\dfrac{\sqrt{x}-2-2\left(\sqrt{x}+2\right)+x}{x-4}\\ =\dfrac{\sqrt{x}-2-2\sqrt{x}-4+x}{x-4}\\ =\dfrac{-\sqrt{x}+x-6}{x-4}\\ =\dfrac{2\sqrt{x}+x-3\sqrt{x}-6}{x-4}\\ =\dfrac{\sqrt{x}\left(2+\sqrt{x}\right)-3\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{\sqrt{x}-3}{\sqrt{x}-2}\)
\(x=16\Rightarrow A=\dfrac{\sqrt{16}-3}{\sqrt{16}-2}=\dfrac{1}{2}\)
\(c,A=\dfrac{2}{3}\Leftrightarrow\dfrac{\sqrt{x}-3}{\sqrt{x}-2}=\dfrac{2}{3}\\ \Rightarrow3\left(\sqrt{x}-3\right)=2\left(\sqrt{x}-2\right)\\ \Rightarrow3\sqrt{x}-9=2\sqrt{x}-4\)
\(\Rightarrow\sqrt{x}=5\\ \Rightarrow x=25\left(tmdk\right)\)
Vậy ...
Đúng 2
Bình luận (0)
3:
1: \(x-7=\left(\sqrt{x}-\sqrt{7}\right)\left(\sqrt{x}+\sqrt{7}\right)\)
2: \(2+x=2-\left(-x\right)=\left(\sqrt{2}-\sqrt{-x}\right)\left(\sqrt{2}+\sqrt{-x}\right)\)
3: \(x-6\sqrt{x}+9=\left(\sqrt{x}-3\right)^2\)
4: \(=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)-\left(\sqrt{x}+\sqrt{y}\right)\)
=(căn x+căn y)(căn x-căn y-1)
5: \(x\sqrt{y}-y\sqrt{x}=\sqrt{xy}\left(\sqrt{x}-\sqrt{y}\right)\)
6: \(x\sqrt{x}+1=\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)\)
7: \(x-5\sqrt{x}+6=\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)\)
8: \(x-\sqrt{x}-2=\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)
9: \(=2^3-\left(\sqrt{x}\right)^3=\left(2-\sqrt{x}\right)\left(4+2\sqrt{x}+x\right)\)
2:
1: 5căn 11>5*căn 9=15
=>-5căn 11<-15
2: 2căn 2<3
=>7+2*căn 2<7+3
=>7+2*căn 2<10
3: 2căn 3=căn 12
3*căn 2=căn 18
=>2*căn 3<3*căn 2
=>\(\sqrt{2\sqrt{3}}< \sqrt{3\sqrt{2}}\)
Đúng 0
Bình luận (0)
Bài 3: Cho a,b,c dương thỏa mãn abc8. Tính giá trị biểu thức
Đọc tiếp
Bài 3: Cho a,b,c dương thỏa mãn abc=8. Tính giá trị biểu thức ![]()
Hình load lên không xem được. Bạn nên gõ đề để được hỗ trợ tốt hơn nhé.
Đúng 0
Bình luận (0)
\(\dfrac{\sqrt{2}-1}{\sqrt{2}+1}-\dfrac{3-\sqrt{2}}{3+\sqrt{2}}\)
\(\dfrac{1}{\sqrt{2}-\sqrt{3}}-\dfrac{3}{\sqrt{18}+2\sqrt{3}}\)
\(\dfrac{\sqrt{2}-1}{\sqrt{2}+1}-\dfrac{3-\sqrt{2}}{3+\sqrt{2}}\\ =\dfrac{\left(\sqrt{2}-1\right)^2}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}-\dfrac{\left(3-\sqrt{2}\right)^2}{\left(3+\sqrt{2}\right)\left(3-\sqrt{2}\right)}\\ =\dfrac{3-2\sqrt{2}}{2-1}-\dfrac{11-6\sqrt{2}}{9-2}\\ =3-2\sqrt{2}-\dfrac{11-6\sqrt{2}}{7}\\ =\dfrac{7\left(3-2\sqrt{2}\right)-\left(11-6\sqrt{2}\right)}{7}\\ =\dfrac{21-14\sqrt{2}-11+6\sqrt{2}}{7}\\ =\dfrac{10-8\sqrt{2}}{7}\)
\(\dfrac{1}{\sqrt{2}-\sqrt{3}}-\dfrac{3}{\sqrt{18}+2\sqrt{3}}\\ =\dfrac{1}{\sqrt{2}-\sqrt{3}}-\dfrac{3}{3\sqrt{2}+2\sqrt{3}}\\ =\dfrac{3\sqrt{2}+2\sqrt{3}-3\sqrt{2}+3\sqrt{3}}{\left(\sqrt{2}-\sqrt{3}\right)\left[\sqrt{6}\left(\sqrt{2}+\sqrt{3}\right)\right]}\\ =\dfrac{5\sqrt{3}}{\sqrt{6}\left(3-2\right)}\\ =\dfrac{5\sqrt{3}}{\sqrt{2}.\sqrt{3}}\\ =\dfrac{5}{\sqrt{2}}\)
Đúng 1
Bình luận (0)