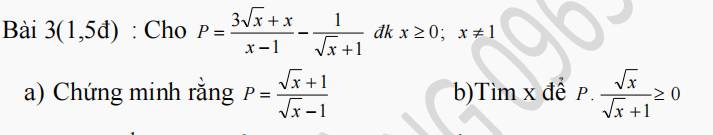\(a,P=\dfrac{3\sqrt{x}+x}{x-1}-\dfrac{1}{\sqrt{x}+1}\left(dk:x\ge0,x\ne1\right)\)
\(=\dfrac{3\sqrt{x}+x}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}+1}\\ =\dfrac{3\sqrt{x}+x-\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{2\sqrt{x}+x+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\left(dpcm\right)\)
\(b,P.\dfrac{\sqrt{x}}{\sqrt{x}+1}\ge0\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-1}.\dfrac{\sqrt{x}}{\sqrt{x}+1}\ge0\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-1}\ge0\\ \Leftrightarrow x\ge0\)
Vậy \(x\ge0\) thì thỏa mãn đề bài.
Đúng 0
Bình luận (0)