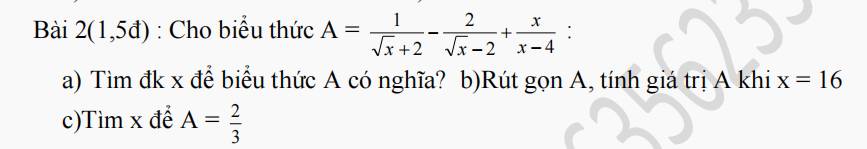\(a,\) A có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}x\ge0\\x\ne4\end{matrix}\right.\)
\(b,A=\dfrac{1}{\sqrt{x}+2}-\dfrac{2}{\sqrt{x}-2}+\dfrac{x}{x-4}\\ =\dfrac{\sqrt{x}-2-2\left(\sqrt{x}+2\right)+x}{x-4}\\ =\dfrac{\sqrt{x}-2-2\sqrt{x}-4+x}{x-4}\\ =\dfrac{-\sqrt{x}+x-6}{x-4}\\ =\dfrac{2\sqrt{x}+x-3\sqrt{x}-6}{x-4}\\ =\dfrac{\sqrt{x}\left(2+\sqrt{x}\right)-3\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{\sqrt{x}-3}{\sqrt{x}-2}\)
\(x=16\Rightarrow A=\dfrac{\sqrt{16}-3}{\sqrt{16}-2}=\dfrac{1}{2}\)
\(c,A=\dfrac{2}{3}\Leftrightarrow\dfrac{\sqrt{x}-3}{\sqrt{x}-2}=\dfrac{2}{3}\\ \Rightarrow3\left(\sqrt{x}-3\right)=2\left(\sqrt{x}-2\right)\\ \Rightarrow3\sqrt{x}-9=2\sqrt{x}-4\)
\(\Rightarrow\sqrt{x}=5\\ \Rightarrow x=25\left(tmdk\right)\)
Vậy ...