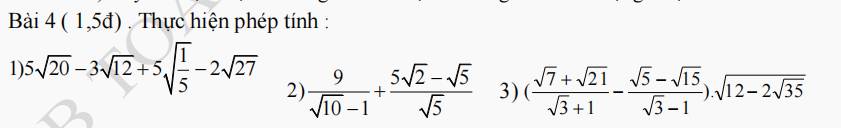1) \(5\sqrt{20}-3\sqrt{12}+5\sqrt{\dfrac{1}{5}}-2\sqrt{27}\)
\(=5\cdot2\sqrt{5}-3\cdot2\sqrt{3}+\sqrt{25\cdot\dfrac{1}{5}}-2\cdot3\sqrt{3}\)
\(=10\sqrt{5}-6\sqrt{3}+\sqrt{5}-6\sqrt{3}\)
\(=11\sqrt{5}\)
2) \(\dfrac{9}{\sqrt{10}-1}+\dfrac{5\sqrt{2}-\sqrt{5}}{\sqrt{5}}\)
\(=\dfrac{9\left(\sqrt{10}+1\right)}{\left(\sqrt{10}-1\right)\left(\sqrt{10}+1\right)}+\dfrac{\sqrt{5}\left(\sqrt{10}-1\right)}{\sqrt{5}}\)
\(=\dfrac{9\left(\sqrt{10}+1\right)}{10-1}+\sqrt{10}-1\)
\(=\sqrt{10}+1+\sqrt{10}-1\)
\(=2\sqrt{10}\)
3) \(\left(\dfrac{\sqrt{7}-\sqrt{21}}{\sqrt{3}+1}-\dfrac{\sqrt{5}-\sqrt{15}}{\sqrt{3}-1}\right)\cdot\sqrt{12-2\sqrt{35}}\)
\(=\left(\dfrac{\sqrt{7}\left(1+\sqrt{3}\right)}{\sqrt{3}+1}-\dfrac{\sqrt{5}\left(1-\sqrt{3}\right)}{\sqrt{3}-1}\right)\sqrt{12-2\sqrt{35}}\)
\(=\left(\sqrt{7}+\sqrt{5}\right)\sqrt{\left(\sqrt{7}\right)^2-2\cdot\sqrt{7}\cdot\sqrt{5}+\left(\sqrt{5}\right)^2}\)
\(=\left(\sqrt{7}+\sqrt{5}\right)\sqrt{\left(\sqrt{7}-\sqrt{5}\right)^2}\)
\(=\left(\sqrt{7}+\sqrt{5}\right)\left|\sqrt{7}-\sqrt{5}\right|\)
\(=\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
\(=\left(\sqrt{7}\right)^2-\left(\sqrt{5}\right)^2\)
\(=7-5\)
\(=2\)
1: \(=5\cdot2\sqrt{5}-3\cdot2\sqrt{3}-2\cdot3\sqrt{3}+\sqrt{5}\)
=11căn 5-12căn 3
2: \(=\sqrt{10}+1+\sqrt{10}-1=2\sqrt{10}\)
3: \(=\left(\dfrac{\sqrt{7}\left(\sqrt{3}+1\right)}{\sqrt{3}+1}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\right)\cdot\left(\sqrt{7}-\sqrt{5}\right)\)
=(căn 7+căn 5)(căn 7-căn 5)
=7-5
=2