Bài 1: Căn bậc hai

Sửa đề: \(x^2-2mx+2m-1=0\)

\(\Delta=\left(-2m\right)^2-4\cdot1\cdot\left(2m-1\right)\)

\(=4m^2-8m+4=\left(2m-2\right)^2\)

Để phương trình có hai nghiệm phân biệt thì \(\Delta>0\)

=>\(\left(2m-2\right)^2>0\)

=>\(2m-2\ne0\)

=>\(2m\ne2\)

=>\(m\ne1\)

Theo Vi-et, ta có: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left(-2m\right)}{1}=2m\\x_1\cdot x_2=\dfrac{c}{a}=2m-1\end{matrix}\right.\)

Để hai nghiệm phân biệt cùng dương thì \(\left\{{}\begin{matrix}x_1+x_2>0\\x_1x_2>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m>0\\2m-1>0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{2}\)

trả lời giúp mik đi ạ 

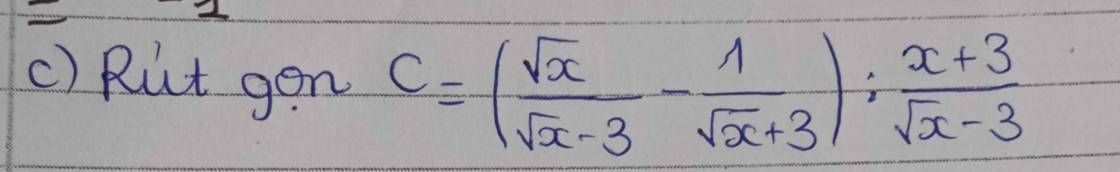
Lời giải:

ĐKXĐ: $x\geq 0; x\neq 9$

\(C=\frac{\sqrt{x}(\sqrt{x}+3)-(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}+3)}.\frac{\sqrt{x}-3}{x+3}\\ =\frac{x+2\sqrt{x}+3}{(\sqrt{x}-3)(\sqrt{x}+3)}.\frac{\sqrt{x}-3}{x+3}=\frac{x+2\sqrt{x}+3}{(\sqrt{x}+3)(x+3)}\)

ĐKXĐ: x>=11

\(\sqrt{25x-275}-\sqrt{9x-99}-\sqrt{x-11}=1\)

=>\(\sqrt{25\left(x-11\right)}-\sqrt{9\left(x-11\right)}-\sqrt{x-11}=1\)

=>\(5\sqrt{x-11}-3\sqrt{x-11}-\sqrt{x-11}=1\)

=>\(\sqrt{x-11}=1\)

=>x-11=1

=>x=12(nhận)

a: Thay h=65 vào \(d=3,57\sqrt{h}\), ta được:

\(d=3,57\cdot\sqrt{65}\simeq28,78\left(km\right)\)

b: Đặt \(d=30\left(km\right)\)

=>\(3,57\cdot\sqrt{h}=30\)

=>\(\sqrt{h}=\dfrac{30}{3,57}\)

=>\(h\simeq70,62\left(m\right)\)

b: \(\sqrt{33-12\sqrt{6}}+\sqrt{\left(3-\sqrt{6}\right)^2}\)

\(=\sqrt{24-2\cdot2\sqrt{6}\cdot3+9}+\sqrt{\left(3-\sqrt{6}\right)^2}\)

\(=\sqrt{\left(2\sqrt{6}-3\right)^2}+\left|3-\sqrt{6}\right|\)

\(=\left|2\sqrt{6}-3\right|+3-\sqrt{6}\)

\(=2\sqrt{6}-3+3-\sqrt{6}\)

\(=\sqrt{6}\)

c: \(\dfrac{5\sqrt{3}+3\sqrt{5}}{\sqrt{3}+\sqrt{5}}-\dfrac{11}{\sqrt{15}-2}\)

\(=\dfrac{\sqrt{15}\cdot\sqrt{5}+\sqrt{15}\cdot\sqrt{3}}{\sqrt{5}+\sqrt{3}}-\dfrac{11\left(\sqrt{15}+2\right)}{11}\)

\(=\dfrac{\sqrt{15}\left(\sqrt{5}+\sqrt{3}\right)}{\sqrt{5}+\sqrt{3}}-\left(\sqrt{15}+2\right)\)

\(=\sqrt{15}-\sqrt{15}-2=-2\)

1: ΔAHB vuông tại H có HM là đường cao

nên \(AM\cdot AB=AH^2\left(1\right)\)

Xét ΔAHC vuông tại H có HN là đường cao

nên \(AN\cdot AC=AH^2\left(2\right)\)

Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

=>\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)

Xét ΔAMN và ΔACB có

\(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)

\(\widehat{MAN}\) chung

Do đó: ΔAMN đồng dạng vớiΔACB

\(=\dfrac{\sqrt{a}+1}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}-\dfrac{\sqrt{a}-1}{\left(\sqrt{a}+2\right)^2}\left(\dfrac{\sqrt{a}\left(a+2\sqrt{a}-4\right)-2}{\sqrt{a}}\right)\\ =\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}+2\right)-\left[\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)\right]}{\left(\sqrt{a}+2\right)^2\left(\sqrt{a}-2\right)}.\left(a+2\sqrt{a}+1-5\right)-2\\ =\dfrac{a+3\sqrt{a}+2-a+3\sqrt{a}+2}{\left(\sqrt{a}+2\right)^2\left(\sqrt{a}-2\right)}\left(\sqrt{a}+2\right)^2-7\)   

\(=\dfrac{6\sqrt{a}+4}{\sqrt{a}-2}-7=\dfrac{6\sqrt{a}+4-7\sqrt{a}+14}{\sqrt{a}-2}\\ =\dfrac{-\sqrt{a}+18}{\sqrt{a}-2}\)

\(\left(\dfrac{\sqrt{a}+1}{a-4}-\dfrac{\sqrt{a}-1}{a+4\sqrt{a}+4}\right)\left(\dfrac{a\sqrt{a}+2a-4\sqrt{a}-2}{\sqrt{a}}\right)\)
\(=\left[\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}+2\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)^2}-\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)^2}\right]\left[\dfrac{a\sqrt{a}+2a-4\sqrt{a}-2}{\sqrt{a}}\right]\)
\(=\dfrac{a+3\sqrt{a}+2-a+3\sqrt{a}+2}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)^2}\left[\dfrac{a\sqrt{a}+2a-4\sqrt{a}-2}{\sqrt{a}}\right]\)
\(=\dfrac{6\sqrt{a}+4}{\left(\sqrt{a}-2\right)\left(a+4\sqrt{a}+4\right)}\left(\dfrac{a\sqrt{a}+2a-4\sqrt{a}-2}{\sqrt{a}}\right)\)
\(=\dfrac{6\sqrt{a}+4}{a\sqrt{a}+4a+4\sqrt{a}-2a-8\sqrt{a}-8}\left(\dfrac{a\sqrt{a}+2a-4\sqrt{a}-2}{\sqrt{a}}\right)\)
\(=\dfrac{6\sqrt{a}+4}{a\sqrt{a}+2a-4\sqrt{a}-8}\left(\dfrac{a\sqrt{a}+2a-4\sqrt{a}-8+6}{\sqrt{a}}\right)\)
\(=\dfrac{ }{ }\)\(\dfrac{\left(6\sqrt{a}+4\right)\left(a\sqrt{a}+2a-4\sqrt{a}-8\right)}{\left(a\sqrt{a}+2a-4\sqrt{a}-8\right)\sqrt{a}}+\dfrac{\left(6\sqrt{a}+4\right).6}{\left(a\sqrt{a}+2a-4\sqrt{a}-8\right)\sqrt{a}}\)
\(=\dfrac{6\sqrt{a}+4}{\sqrt{a}}+\dfrac{36\sqrt{a}+24}{\sqrt{a}\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)^2}\)??????
 

=⎡⎣(√a+1)(√a+2)(√a−2)(√a+2)2−(√a−1)(√a−2)(√a−2)(√a+2)2⎤⎦[a√a+2a−4√a−2√a]=[(�+1)(�+2)(�−2)(�+2)2−(�−1)(�−2)(�−2)(�+2)2][��+2�−4�−2�]
=6√a+4(√a−2)(a+4√a+4)(a√a+2a−4√a−2√a)=6�+4(�−2)(�+4�+4)(��+2�−4�−2�)
=6√a+4a√a+2a−4√a−8(a√a+2a−4√a−8+6√a)=6�+4��+2�−4�−8(��+2�−4�−8+6�)
(6√a+4)(a√a+2a−4√a−8)(a√a+2a−4√a−8)√a+(6√a+4).6(a√a+2a−4√a−8)√a(6�+4)(��+2�−4�−8)(��+2�−4�−8)�+(6�+4).6(��+2�−4�−8)�

\(\dfrac{1}{\sqrt{5}-\sqrt{3}}+\dfrac{5\sqrt{3}-3\sqrt{5}}{2\sqrt{15}-\sqrt{20}}\)

\(=\dfrac{1}{\sqrt{5}-\sqrt{3}}+\dfrac{5\sqrt{3}-3\sqrt{5}}{2\left(\sqrt{15}-\sqrt{5}\right)}\)

\(=\dfrac{2\sqrt{15}-2\sqrt{5}+\sqrt{15}\left(8-2\sqrt{15}\right)}{2\sqrt{5}\left(\sqrt{3}-1\right)\left(\sqrt{5}-\sqrt{3}\right)}\)

\(=\dfrac{2\sqrt{15}-2\sqrt{5}+8\sqrt{15}-30}{2\sqrt{5}\left(\sqrt{3}-1\right)\left(\sqrt{5}-\sqrt{3}\right)}\)

\(=\dfrac{10\sqrt{15}-2\sqrt{5}-30}{2\sqrt{5}\left(\sqrt{3}-1\right)\left(\sqrt{5}-\sqrt{3}\right)}\)

\(=\dfrac{2\sqrt{5}\left(5\sqrt{3}-1-3\sqrt{5}\right)}{2\sqrt{5}\left(\sqrt{3}-1\right)\left(\sqrt{5}-\sqrt{3}\right)}=\dfrac{5\sqrt{3}-3\sqrt{5}-1}{\left(\sqrt{3}-1\right)\left(\sqrt{5}-\sqrt{3}\right)}\)

\(\dfrac{1}{\sqrt{5}-\sqrt{3}}+\dfrac{5\sqrt{3}-3\sqrt{5}}{2\sqrt{15}-\sqrt{20}}\)

\(=\dfrac{\sqrt{5}+\sqrt{3}}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}+\dfrac{\sqrt{15}\left(\sqrt{5}-\sqrt{3}\right)}{2\sqrt{5}\left(\sqrt{3}-1\right)}\)

\(=\dfrac{\sqrt{5}+3}{5-3}+\dfrac{\sqrt{3}\left(\sqrt{5}-\sqrt{3}\right)}{2\left(\sqrt{3}-1\right)}\)

\(=\dfrac{\sqrt{5}+\sqrt{3}}{2}+\dfrac{\left(\sqrt{15}-3\right)\left(\sqrt{3}+1\right)}{2\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)

\(=\dfrac{\sqrt{5}+\sqrt{3}}{2}+\dfrac{3\sqrt{5}+\sqrt{15}-3\sqrt{3}-3}{2\cdot2}\)

\(=\dfrac{2\sqrt{5}+2\sqrt{3}+3\sqrt{5}+\sqrt{15}-3\sqrt{3}-3}{4}\)

\(=\dfrac{5\sqrt{5}-\sqrt{3}+\sqrt{15}-3}{4}\)

\(\sqrt{x+2\sqrt{x-1}}=2x-1\left(Đk:x\ge1\right)\)

\(\sqrt{x-1+2\sqrt{x-1}+1}=2x-1\)

\(\sqrt{\left(\sqrt{x-1}+1\right)^2}=2x-1\)

\(\sqrt{x-1}+1=2x-1\)

\(\sqrt{x-1}=2\left(x-1\right)\)

\(\sqrt{x-1}\left(2\sqrt{x-1}-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-1}=0\\2\sqrt{x-1}-1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\4\left(x-1\right)=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{4}\end{matrix}\right.\)

\(\sqrt{x+2\sqrt{x-1}}=2x-1\) \(\left(x\ge1\right)\)

\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}\right)^2+2\cdot\sqrt{x-1}\cdot1+1^2}=2x-1\)

\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}+1\right)^2}=2x-1\)

\(\Leftrightarrow\left|\sqrt{x-1}+1\right|=2x-1\)  

Vì: \(\sqrt{x-1}+1>0.khi.x\ge1\)  

\(\Leftrightarrow\sqrt{x-1}+1=2x-1\)

\(\Leftrightarrow\sqrt{x-1}=2x-1-1\)

\(\Leftrightarrow\sqrt{x-1}=2x-2\)

\(\Leftrightarrow\sqrt{x-1}=2\left(x-1\right)\)

\(\Leftrightarrow\sqrt{x-1}-2\left(\sqrt{x-1}\right)^2=0\)

\(\Leftrightarrow\sqrt{x-1}\left(1-2\sqrt{x-1}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-1}=0\\1-2\sqrt{x-1}=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2\sqrt{x-1}=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\sqrt{x-1}=\dfrac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x-1=\dfrac{1}{4}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{4}+1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{4}\end{matrix}\right.\left(tm\right)\) 

Vậy: \(S=\left\{1;\dfrac{5}{4}\right\}\)

Lời giải:
1. ĐKXĐ: $-2x+3\geq 0\Leftrightarrow 3\geq 2x$

$\Leftrightarrow x\leq \frac{3}{2}$

2. ĐKXĐ: \(\left\{\begin{matrix} x^2\neq 0\\ \frac{2}{x^2}\geq 0\end{matrix}\right.\Leftrightarrow x^2\neq 0\Leftrightarrow x\neq 0\)

3. ĐKXĐ: \(\left\{\begin{matrix} x+3\neq 0\\ \frac{4}{x+3}\geq 0\end{matrix}\right.\Leftrightarrow x+3>0\Leftrightarrow x> -3\)

4. ĐKXĐ: \(\left\{\begin{matrix} x^2+6\neq 0\\ \frac{-5}{x^2+6}\geq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x^2+6\neq 0\\ x^2+6<0\end{matrix}\right.\Leftrightarrow x^2+6<0\) (vô lý)

Vậy biểu thức không xác định với mọi $x\in\mathbb{R}$

5. ĐKXĐ: $3x+4\geq 0\Leftrightarrow x\geq \frac{-4}{3}$

6. ĐKXĐ: $x^2+1\geq 0\Leftrightarrow x\in\mathbb{R}$
7. ĐKXĐ: \(\left\{\begin{matrix} 1-2x\neq 0\\ \frac{3}{1-2x}\geq 0\end{matrix}\right.\Leftrightarrow 1-2x>0\Leftrightarrow x< \frac{1}{2}\)

8. ĐKXĐ: \(\left\{\begin{matrix} 3x+5\neq 0\\ \frac{-3}{3x+5}\geq 0\end{matrix}\right.\Leftrightarrow 3x+5<0\Leftrightarrow x< \frac{-5}{3}\)