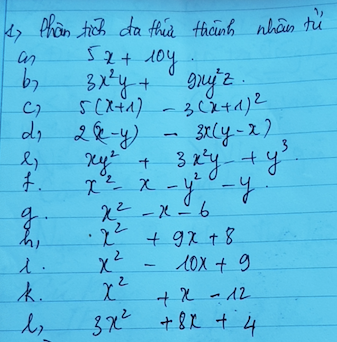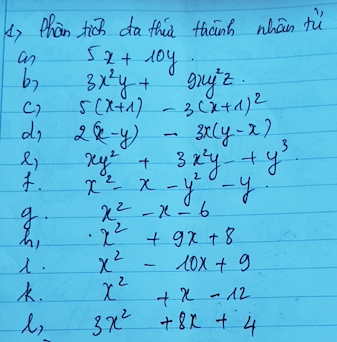a,\(5x+10y=5\left(x+2y\right)\)
b,\(=3xy\left(x+3yz\right)\)
c,\(=\left(x+1\right)\left(5-3x-3\right)=\left(x+1\right)\left(2-3x\right)\)
d,\(=\left(x-y\right)\left(2+3x\right)\)
e,\(=y\left(xy+3x^2+y^2\right)\)
f,\(=\left(x-y\right)\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(x-y-1\right)\)
g,\(=x^2-x+\dfrac{1}{4}-\left(\dfrac{5}{2}\right)^2=\left(x-\dfrac{1}{2}\right)^2-\left(\dfrac{5}{2}\right)^2=\left(x-3\right)\left(x+2\right)\)
h,\(=x^2+9x+\dfrac{81}{4}-\left(\dfrac{7}{2}\right)^2=\left(x+\dfrac{9}{2}\right)^2-\left(\dfrac{7}{2}\right)^2=\left(x+1\right)\left(x+8\right)\)
i,\(=x^2-10x+25-4^2=\left(x-5\right)^2-4^2=\left(x-1\right)\left(x-9\right)\)
k,\(=x^2+x+\dfrac{1}{4}-\left(\dfrac{7}{2}\right)^2=\left(x+\dfrac{1}{2}\right)^2-\left(\dfrac{7}{2}\right)^2=\left(x-3\right)\left(x+4\right)\)
l.\(=3\left(x^2+\dfrac{8}{3}x+\dfrac{4}{3}\right)=3\left(x^2+\dfrac{8}{3}x+\dfrac{16}{9}-\dfrac{4}{9}\right)\)
\(=3[\left(x+\dfrac{4}{3}\right)^2-\left(\dfrac{2}{3}\right)^2]=3\left(x+\dfrac{2}{3}\right)\left(x+2\right)\)
A, 5(x+2y)
B, 3xy(x+3yz)
C, (x+1)[5-3(x+1)]
D, (x-y)(2+3x)
E, y(xy+3x^2+y^2)
F ,(x+y)(x-y-1)
G, (x-3)(x+2)
H, (x+1)(x+8)
I, (x-9)(x-1)
K, (x-3)(x+4)
L, (x+2)(3x+2)
a) \(5x+10y=5\left(x+2y\right)\)
g) \(x^2-x-6=\left(x-3\right)\left(x+2\right)\)
h) \(x^2+9x+8=\left(x+1\right)\left(x+8\right)\)
i) \(x^2-10x+9=\left(x-1\right)\left(x-9\right)\)
k) \(x^2+x-12=\left(x+4\right)\left(x-3\right)\)
l) \(3x^2+8x+4=\left(x+2\right)\left(3x+2\right)\)