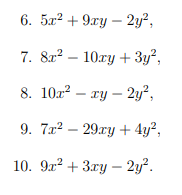\(6,=5x^2-xy+10xy-2y^2=x\left(5x-y\right)+2y\left(5x-y\right)=\left(x+2y\right)\left(5x-y\right)\\ 7,=8x^2-4xy-6xy+3y^2=4x\left(2x-y\right)-3y\left(2x-y\right)=\left(4x-3y\right)\left(2x-y\right)\\ 8,=10x^2-5xy+4xy-2y^2=5x\left(2x-y\right)+2y\left(2x-y\right)=\left(5x+2y\right)\left(2x-y\right)\\ 9,=7x^2-28xy-xy+4y^2=7x\left(x-4y\right)-y\left(x-4y\right)=\left(7x-y\right)\left(x-4y\right)\\ 10,=9x^2-3xy+6xy-2y^2=3x\left(3x-y\right)+2y\left(3x-y\right)=\left(3x+2y\right)\left(3x-y\right)\)
6) \(5x^2+10xy-xy-2y^2\)
\(=5x\left(x+2y\right)-y\left(x+2y\right)\)
\(=\left(x+2y\right)\left(5x-y\right)\)
7) \(8x^2-10xy+3y^2=4x\left(2x-3y\right)-y\left(2x-3y\right)=\left(2x-3y\right)\left(4x-y\right)\)
8) \(10x^2-xy-2y^2=5x\left(2x-y\right)+2y\left(2x-y\right)=\left(2x-y\right)\left(5x+2y\right)\)
9) \(7x^2-29xy+4y^2=7x\left(x-4y\right)-y\left(x-4y\right)=\left(x-4y\right)\left(7x-y\right)\)
10) \(9x^2+3xy-2y^2=3x\left(3x-y\right)+2y\left(3x-y\right)=\left(3x-y\right)\left(3x+2y\right)\)