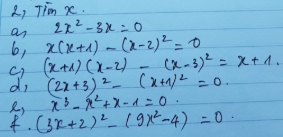a) x² - 6x + 9
= x² - 2.x.3 + 3²
= (x - 3)²
b) x² - 6
= x² - (√6)²
= (x - √6)(x + √6)
c) 1 - 27x³
= 1³ - (3x)³
= (1 - 3x)(1 + 3x + 9x²)
d) x³ + 1/x³
= x³ + (1/x)³
= (x + 1/x)(x² - 1 + 1/x²)
e) -x³ + 9x² - 27x + 27
= -(x³ - 3.x².3 + 3.x.3² - 3³)
= -(x - 3)³
a)
\(x^2-6x+9=x^2-2.x.3+3^2\\ =\left(x-3\right)^2\)
b)
\(x^2-9\) mới đúng đề chứ
\(=x^2-3^2\\ =\left(x-3\right)\left(x+3\right)\)
Hoặc với `x^2-6` luôn nha:
\(x^2-6\\ =x^2-\left(\sqrt{6}\right)^2\\ =\left(x-\sqrt{6}\right)\left(x+\sqrt{6}\right)\)
c)
\(1-27x^3\\ =1-\left(3x\right)^3\\ =\left(1-3x\right)\left(1+3x+9x^2\right)\)
d)
\(x^3+\dfrac{1}{x^3}\\ =x^3+\left(\dfrac{1}{x}\right)^3\\ =\left(x+\dfrac{1}{x}\right)\left(x^2-1+\dfrac{1}{x^2}\right)\)
e)
\(-x^2+9x^2-27x+27\\ =-\left(x^2-9x^2+27x-27\right)\\ =-\left(x^2-3.3x^2+3.3^2.x-3^3\right)\\ =-\left(x-3\right)^3\\ =-\left(x-3\right)\left(x-3\right)\left(x-3\right)\)





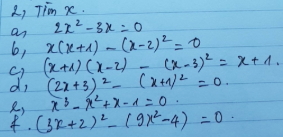 Không làm tắt
Không làm tắt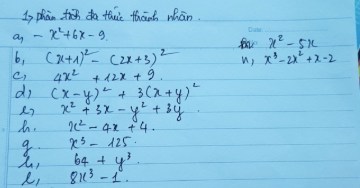 Ko làm tắt
Ko làm tắt