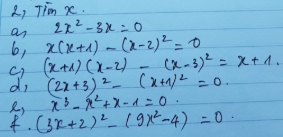a: =(x-5)^2(x+5)^2-(x-5)^2
=(x-5)^2[(x+5)^2-1]
=(x-5)^2*(x+5-1)(x+5+1)
=(x+4)(x+6)(x-5)^2
b: =(2x-5)^2*(2x+5)^2-9(2x-5)^2
=(2x-5)^2[(2x+5)^2-9]
=(2x-5)^2(2x+5-3)(2x+5+3)
=4(x+4)(x+1)(2x-5)^2
c: =(2x-3)^2[4-9(2x+3)^2]
=(2x-3)^2*[2^2-(6x+9)^2]
=(2x-3)(2-6x-9)(2+6x+9)*(2x-3)
=(-6x-7)(11+6x)(2x-3)^2
d: =a^2(a^4-a^2+2a+2)
=a^2[a^2(a-1)(a+1)+2(a+1)]
=a^2(a+1)(a^2-a+2)
e: =(3x^2+3x+2-3x^2-3x+2)(3x^2+3x+2+3x^2+3x-2)
=(6x^2+6x)*4
=24x(x+1)



 Không làm tắt
Không làm tắt Ko làm tắt
Ko làm tắt