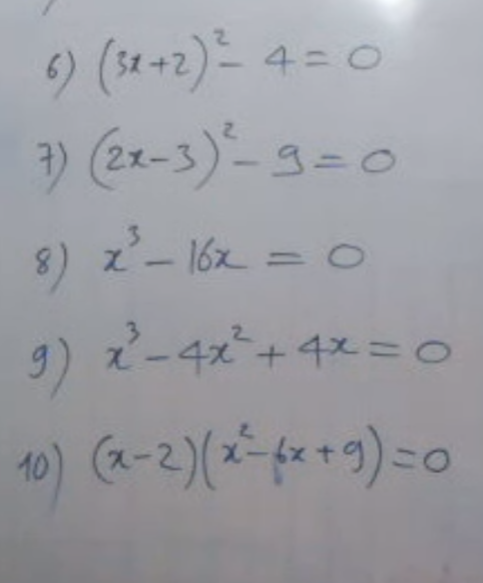6: Ta có: \(\left(3x+2\right)^2-4=0\)
\(\Leftrightarrow3x\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{4}{3}\end{matrix}\right.\)
10: Ta có: \(\left(x-2\right)\left(x^2-6x+9\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
6) \(\Rightarrow\left(3x+2\right)^2=4\)
\(\Rightarrow\left[{}\begin{matrix}3x+2=2\\3x+2=-2\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{4}{3}\end{matrix}\right.\)
7) \(\Rightarrow\left(2x-3\right)^2=9\)
\(\Rightarrow\left[{}\begin{matrix}2x-3=3\\2x-3=-3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=3\\x=0\end{matrix}\right.\)
8) \(\Rightarrow x\left(x-4\right)\left(x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
9) \(\Rightarrow x\left(x-2\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
10) \(\Rightarrow\left(x-2\right)\left(x-3\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
6)\(\left(3x+2\right)^2-4=0\)
\(\left(3x+2\right)^2-2^2=0\)
\(\left(3x+2-2\right)\left(3x+2+2\right)=0\)
\(3x\left(3x+4\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}3x=0\\3x+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=\dfrac{-4}{3}\end{matrix}\right.\)
Vậy...