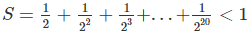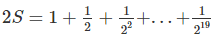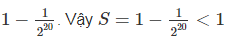chứng minh rằng S = 1/2 + 1/2^2 + 1/2^3+...+1/2^20 <1
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
HM
Những câu hỏi liên quan
Chứng minh rằng:
S=1/2+1/2^2+1/2^3+...+1/2^20<1
S = 1/2 + 1/2² + 1/2³ + ... + 1/2²⁰
⇒2S = 1 + 1/2 + 1/2² + ... + 1/2¹⁹
⇒S = 2S - S
= (1 + 1/2 + 1/2² + ... + 1/2¹⁹) - (1/2 + 1/2² + 1/2³ + ... + 1/2²⁰)
= 1 - 1/2²⁰ < 1
Vậy S < 1
Đúng 1
Bình luận (0)
chứng minh rằng : S=1/2+1/22 +1/ 23 +...1/220 <1
nen 2S=1+1/2+1/2 mu 2 +....1/2 mu 19
do do 2S-S=1-1/2 mu 20 .vay S=1-1/2 mu 20 <1
Đúng 0
Bình luận (0)
chứng minh rằng: S= 1/2+1/2^2+1/2^3+...+1/2^20
Giúp mik vs nha
Chứng minh rằng \(S=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{20}}< 1\)
\(S=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{20}}\)
\(\Rightarrow2S=1+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{19}}\)
\(\Rightarrow2S-S=\left(1+\frac{1}{2^2}+...+\frac{1}{2^{19}}\right)-\left(\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{20}}\right)\)
\(S=1-\frac{2}{2^{20}}\)
\(\Rightarrow S< 1\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Ta có :\(S=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{20}}\)
\(S=\frac{1\cdot2^{19}}{2\cdot2^{19}}+\frac{1\cdot2^{18}}{2^2\cdot2^{18}}+\frac{1\cdot2^{17}}{2^3\cdot2^{17}}+...+\frac{1\cdot2}{2^{19}\cdot2}+\frac{1}{2^{20}}\)
\(S=\frac{2^{19}}{2^{20}}+\frac{2^{18}}{2^{20}}+\frac{2^{17}}{2^{20}}+...+\frac{2}{2^{20}}+\frac{1}{2^{20}}\)
\(S=\frac{2^{19}+2^{18}+2^{17}+...+2^1+1}{2^{20}}\)
\(S=\frac{2^0+2^1+2^2+...+2^{19}}{2^{20}}\)
Xét: Gọi \(N=2^0+2^1+2^2+...+2^{19}\)
\(2\cdot N=2^1\cdot2^2\cdot2^3\cdot...\cdot2^{20}\)
\(2\cdot N-N=\left(2^1+2^2+2^3+...+2^{20}\right)-\left(2^0+2^1+2^2+...+2^{19}\right)\)
\(N=2^{20}-2^0\)
Thay N vào S, ta có :
\(S=\frac{2^{20}-2^0}{2^{20}}\)
\(S=\frac{2^{20}}{2^{20}}-\frac{1}{2^{20}}\)
\(S=1-\frac{1}{2^{20}}\)
Vì \(1-\frac{1}{2^{20}}< 1\Rightarrow S< 1\left(Đpcm\right).\)
Vậy : \(S< 1.\)
Đúng 0
Bình luận (0)
Chứng minh rằng:
\(S=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{20}}<2\)
Bạn nhân S với 2
Lấy 2S-S=1-1/(2^20)
S=1/(2^20) nên < 2
Cần làm đầy đủ hơn thì bảo mình
Đúng 0
Bình luận (0)
Ta có : 1/2 < 1
1/2^2 < 1/2
..............
1/2^19 < 1/2^20
Suy ra 1/2+1/2^2+......+1/2^19<1+1/2+1/2^2+......+1/2^20
Suy ra 1/2+1/2^2+.......+1/2^19+1/2^20<1+1/2+1/2^2+.....+1/2^20+1/2^20
Suy ra S<S+1+1/2^20
Suy ra S<S+1+1/2^20<2
Suy ra S<2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Chứng minh rằng :
S = \(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+....+\frac{1}{2^{20}}<1\)
Ta có: S = 1/ 2 + 1/ 2^2 + 1/ 2^3 + ... + 1/ 2^20
Nên 2S = 1 + 1/2 + 1 / 2^2 + 1/ 2^3 + .... + 1/ 2^19
Do đó 2S - S = 1 - 1/ 2^20 < 1
Vậy S < 1
Đúng 0
Bình luận (0)
2S=\(1+\frac{1}{2}+\frac{1}{2^2}+...+\frac{1}{2^{19}}\)
2S-S=1-\(\frac{1}{2^{20}}\)
S=\(1-\frac{1}{2^{20}}<1\)
S<1
Đúng 0
Bình luận (0)
Chứng minh rằng S = \(\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^{20}}\) nhỏ hơn 1
Cho S=1/2+1/3+1/4+...+1/31+1/32 a) chứng minh rằng S>5/2 b) chứng minh rằng S<9/2
`Answer:`
\(S=\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{31}+\frac{1}{32}\)
a) Ta thấy:
\(\frac{1}{3}+\frac{1}{4}>\frac{1}{4}+\frac{1}{4}=\frac{1}{2}\)
\(\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}>\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{1}{2}\)
\(\frac{1}{9}+...+\frac{1}{16}>8.\frac{1}{16}=\frac{1}{2}\)
\(\frac{1}{17}+\frac{1}{18}+...+\frac{1}{32}>16.\frac{1}{32}=\frac{1}{2}\)
\(\Rightarrow S>\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}=\frac{5}{2}\)
b) Ta thấy:
\(\frac{1}{3}+\frac{1}{4}+\frac{1}{5}< 3.\frac{1}{3}\)
\(\frac{1}{6}+...+\frac{1}{11}< 6.\frac{1}{6}\)
\(\frac{1}{12}+...+\frac{1}{23}< 12.\frac{1}{12}\)
\(\frac{1}{24}+...+\frac{1}{32}< 9.\frac{1}{24}\)
\(\Rightarrow S< \frac{1}{2}+1+1+1+\frac{9}{24}=\frac{31}{8}< \frac{9}{2}\)
Chứng minh rằng :
\(S=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{20}}< 1\)
Ta có:
S = \(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{20}}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{19.20}=1-\dfrac{1}{20}< 1\)
Vậy S<1
Đúng 0
Bình luận (0)
Ta có:
S = 12+122+123+...+1220<11.2+12.3+13.4+...+119.20=1−120<112+122+123+...+1220<11.2+12.3+13.4+...+119.20=1−120<1
Vậy S<1
Đúng 0
Bình luận (0)
Xem thêm câu trả lời