cho 3 số dương x,y,z tm \(x^{2017}+y^{2017}+z^{2017}=\) 3
tìm max \(x^2+y^2+z^2\)
TT
Những câu hỏi liên quan
Cho ba số thực dương x, y, z thỏa mãn: xy+yz+zx=2017. chứng minh : \(\sqrt{\dfrac{yz}{x^2+2017}}+\sqrt{\dfrac{zx}{y^2+2017}}+\sqrt{\dfrac{xy}{z^2+2017}}\le\dfrac{3}{2}\)
Ta có:\(\sqrt{\dfrac{yz}{x^2+2017}}=\sqrt{\dfrac{yz}{x^2+xy+yz+zx}}=\sqrt{\dfrac{yz}{\left(x+y\right)\left(x+z\right)}}\)
\(=\sqrt{\dfrac{y}{x+y}\cdot\dfrac{z}{x+z}}\le\dfrac{\dfrac{y}{x+y}+\dfrac{z}{x+z}}{2}\)
Tương tự ta có:\(\sqrt{\dfrac{zx}{y^2+2017}}\le\dfrac{\dfrac{x}{x+y}+\dfrac{z}{y+z}}{2}\)
\(\sqrt{\dfrac{xy}{z^2+2017}}\le\dfrac{\dfrac{y}{z+y}+\dfrac{x}{x+z}}{2}\)
Cộng vế với vế ta có:
\(\sqrt{\dfrac{yz}{x^2+2017}}+\sqrt{\dfrac{zx}{y^2+2017}}+\sqrt{\dfrac{xy}{z^2+2017}}\)
\(\le\dfrac{\dfrac{y}{x+y}+\dfrac{z}{x+z}+\dfrac{z}{z+y}+\dfrac{x}{x+y}+\dfrac{y}{z+y}+\dfrac{x}{x+z}}{2}\)
\(=\dfrac{\dfrac{x+y}{x+y}+\dfrac{y+z}{y+z}+\dfrac{z+x}{z+x}}{2}=\dfrac{1+1+1}{2}=\dfrac{3}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=z=\dfrac{\sqrt{2017}}{\sqrt{3}}\)
Đúng 1
Bình luận (1)
x,y,z là các số tự nhiên tm x+y+z=2017 . Tìm max(xyz)
Vì x, y, z là số tự nhiên nên không mất tính tổng quát ta giả sử:
\(x\ge y\ge z\ge0\)
\(\Rightarrow x=2017-y-z\ge2017-0-0=2017\)
Vậy GTLN là 2017 đạt được khi \(\hept{\begin{cases}x=2017\\y=z=0\end{cases}}\) và các hoán vị của nó
Đúng 0
Bình luận (0)
Ở trên a ghi nhầm dấu \(\le\) thành dấu \(\ge\) e sửa hộ a nhé
Đúng 0
Bình luận (0)
ta sẽ chứng minh rằng max của P = xyz đạt được khi các giá trị x, y, z hơn kém nhau không quá 1 đơn vị.
thật vậy, giả sử x0, y0,z0 là các giá trị để P đạt max(tức Max P = x0y0z0) và x0 - y0 \(\ge\) 1 hay x0 - y0 - 1 \(\ge\)1
xét các giá trị x1 = x0 - 1; y1 = y0 + 1, z1 = z0.
khi đó P = z0.(x0 - 1)(y0 +1) = z0(x0y0 +x0 - y0 - 1) > x0y0z0. (vô lí vì x0y0z0 là max P).
vậy khi đó x0, y0, z0 hơn kém nhau không quá 1 đơn vị hay x0 = 672, y0 = 672, z0 = 673. từ đó suy ra maxP.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1: Cho \(a^3+b^3+c^3=3abc\) trong đó a,b,c dương
Tính\(A=\frac{a^{2017}}{b^{2017}}+\frac{b^{2017}}{c^{2017}}+\frac{c^{2017}}{a^{2017}}\)
Bài 2: Cho x+y+z=0
Tính \(A=\frac{x^2+y^2+z^2}{\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2}\)
Em tham khảo tại đây nhé.
Câu hỏi của Phạm Minh Tuấn - Toán lớp 8 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Ta có \(\left(x+y+z\right)^2=x^2+y^2+z^2+2xy+2yz+2zx\)
Do x + y + z = 0 nên \(\left(x+y+z\right)^2=0\)
\(\Rightarrow x^2+y^2+z^2=-2xy-2yz-2zx\)
Vậy thì \(A=\frac{x^2+y^2+z^2}{2\left(x^2+y^2+z^2\right)-2\left(xy+yz+zx\right)}\)
\(A=\frac{-2\left(xy+yz+zx\right)}{-4\left(xy+yz+zx\right)-2\left(xy+yz+zx\right)}\)
\(A=\frac{-2\left(xy+yz+zx\right)}{-6\left(xy+yz+zx\right)}=\frac{1}{3}\)
Đúng 0
Bình luận (0)
Cho 3 số x, y, z TM: \(\left\{{}\begin{matrix}x+y+z=2017\\\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{1}{2017}\end{matrix}\right.\)
Tính GTBT: \(P=\left(x^{2017}+y^{2017}\right)\left(y^{2019}+z^{2019}\right)\left(z^{2021}+x^{2021}\right)\)
cho a,b,c,x,y,z>0
\(\left\{{}\begin{matrix}x+y+z=a\\x^2+y^2+z^2=b\\a^2=b+3034\end{matrix}\right.\)
tính M=\(x\sqrt{\frac{\left(2017+y^2\right)\left(2017+z^2\right)}{2017+x^2}}+y\sqrt{\frac{\left(2017+x^2\right)\left(2017+z^2\right)}{2017+y^2}}+z\sqrt{\frac{\left(2017+y^2\right)\left(2017+x^2\right)}{2017+z^2}}\)
Xin phép được sủa đề một chút nhé :)
\(\left\{{}\begin{matrix}x+y=z=a\\x^2+y^2+z^2=b\\a^2=b+4034\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2+z^2+2\left(xy+yz+zx\right)=a^2\\x^2+y^2+z^2=b\\a^2-b=4034\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2-b=2\left(xy+yz+zx\right)\\a^2-b=4034\end{matrix}\right.\Leftrightarrow xy+yz+zx=2017\)
\(M=x\sqrt{\frac{\left(2017+y^2\right)\left(2017+z^2\right)}{2017+x^2}}+y\sqrt{\frac{\left(2017+x^2\right)\left(2017+z^2\right)}{2017+y^2}}+z\sqrt{\frac{\left(2017+y^2\right)\left(2017+x^2\right)}{2017+z^2}}\)
\(=x\sqrt{\frac{\left(x+y\right)\left(y+z\right)\left(y+z\right)\left(z+x\right)}{\left(x+y\right)\left(z+x\right)}}+y\sqrt{\frac{\left(x+y\right)\left(z+x\right)\left(y+z\right)\left(z+x\right)}{\left(x+y\right)\left(y+z\right)}}+z\sqrt{\frac{\left(x+y\right)\left(z+x\right)\left(x+y\right)\left(y+z\right)}{\left(y+z\right)\left(z+x\right)}}\)
\(=2\left(xy+yz+zx\right)=4034\)
Đúng 0
Bình luận (0)
1. a,b,c0 và a+b+c2017CM:Sigmadfrac{2017a-a^2}{bc}gesqrt{2}left(Sigmasqrt{dfrac{2017-a}{a}}right)2. cho x,y,z tm: x^2+y^2+z^23CM:8left(2-xright)left(2-yright)left(2-zright)geleft(x+yzright)left(y+zxright)left(z+xyright)3. a,b,c0 và a^2+b^2+c^2ge6CM:Sigmadfrac{1}{1+ab}gedfrac{3}{2}
Đọc tiếp
1. a,b,c>0 và a+b+c=2017
\(CM:\Sigma\dfrac{2017a-a^2}{bc}\ge\sqrt{2}\left(\Sigma\sqrt{\dfrac{2017-a}{a}}\right)\)
2. cho x,y,z tm: \(x^2+y^2+z^2=3\)
\(CM:8\left(2-x\right)\left(2-y\right)\left(2-z\right)\ge\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)\)
3. a,b,c>0 và \(a^2+b^2+c^2\ge6\)
\(CM:\Sigma\dfrac{1}{1+ab}\ge\dfrac{3}{2}\)
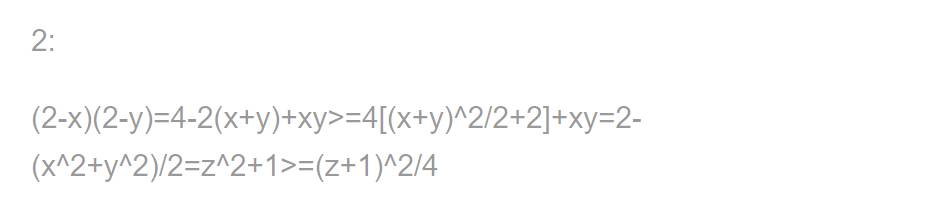
Tương tự, ta được:
\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)
và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)
=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)
(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4
Tương tự, ta cũng co:
\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)
và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)
Do đó, ta được:
\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
=>ĐPCM
Đúng 0
Bình luận (0)
Tính A=( x/2017-z) +( y/2017-x) + (z/2017-y)
biết x+y+z=2017, x,y,z là nguyên dương
cho x,y,z la so thuc thoa man y+z+3/x=x+z+2/y=x+y-3/z=1/x+y+z.
Tinh A=2016.x+y^2017+z^2017
Câu hỏi của Phung Thi Thanh Thao - Toán lớp 7 - Học toán với OnlineMath
Tham khảo tính được x,y,z.Thay vào A
Đúng 0
Bình luận (0)
Cho các số x,y,z thỏa mãn : x^2+y^2+z^2=xy+yz+zx và x^2018 +y^2018+z^2018=3. Tính giá trị của biểu thức P=x^28+y^57+z^2017