so sánh \(\sqrt{2005+2006}và\sqrt{2005}+\sqrt{2006}\)
NP
Những câu hỏi liên quan
so sánh
a\(\sqrt{1999}+\sqrt{2001}\) Và \(2\sqrt{2000}\)
b \(\frac{2006}{\sqrt{2005}}+\frac{2005}{\sqrt{2006}}\)Và \(\sqrt{2005+\sqrt{2006}}\)
so sánh
\(\sqrt{2004}-\sqrt{2003}và\sqrt{2006}-\sqrt{2005}\)
\(\sqrt{2004}-\sqrt{2003}=\dfrac{1}{\sqrt{2004}+\sqrt{2003}}\)
\(\sqrt{2006}-\sqrt{2005}=\dfrac{1}{\sqrt{2006}+\sqrt{2005}}\)
Mà \(\sqrt{2004}+\sqrt{2003}< \sqrt{2006}< \sqrt{2005}\)
\(\Rightarrow\dfrac{1}{\sqrt{2004}+\sqrt{2003}}>\dfrac{1}{\sqrt{2006}+\sqrt{2005}}\)
\(\Rightarrow\sqrt{2004}-\sqrt{2003}>\sqrt{2006}-\sqrt{2005}\)
Đúng 2
Bình luận (0)
so sánh \(\sqrt{2006}-\sqrt{2005}\)và\(\sqrt{2005}-\sqrt{2004}\)
lấy vế đầu trừ vế sau nếu kết quả dương suy ra vế đầu lớn hơn nếu kq âm thì vế sau lớn hơn
Đúng 0
Bình luận (0)
có\(\sqrt{2006}-\sqrt{2005}=\frac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}\)\(=\frac{1}{\sqrt{2006}+\sqrt{2005}}\)
có\(\sqrt{2005}-\sqrt{2004}=\frac{\left(\sqrt{2005}-\sqrt{2004}\right)\left(\sqrt{2005}+\sqrt{2004}\right)}{\sqrt{2005}+\sqrt{2004}}\)\(=\frac{1}{\sqrt{2005}+\sqrt{2004}}\)
ta lại có 2006>2005\(\Rightarrow\sqrt{2006}>\sqrt{2005}\)có 2005>2004\(\Rightarrow\sqrt{2005}>\sqrt{2004}\)
\(\Rightarrow\sqrt{2006}+\sqrt{2005}>\sqrt{2005}+\sqrt{2004}\)\(\Rightarrow\frac{1}{\sqrt{2006}+\sqrt{2005}}< \frac{1}{\sqrt{2005}+\sqrt{2004}}\)
\(\Rightarrow\sqrt{2006}-\sqrt{2005}>\sqrt{2005}-\sqrt{2004}\)
Đúng 0
Bình luận (0)
\(\sqrt{2006}-\sqrt{2005}và\sqrt{2008}-\sqrt{2007}\)
So sánh
Easy
Ta có:
\(\sqrt{2006}-\sqrt{2005}=\frac{2006-2005}{\sqrt{2006}+\sqrt{2005}}=\frac{1}{\sqrt{2006}+\sqrt{2005}}\)
Tương tự cũng có: \(\frac{1}{\sqrt{2007}+\sqrt{2008}}\)
Dễ thấy: \(\sqrt{2005}+\sqrt{2006}< \sqrt{2007}+\sqrt{2008}\)
\(\Rightarrow\frac{1}{\sqrt{2006}+\sqrt{2005}}>\frac{1}{\sqrt{2007}+\sqrt{2008}}\)
Đúng 0
Bình luận (0)
Easy
Ta có:
\(\sqrt{2006}-\sqrt{2005}=\frac{2006-2005}{\sqrt{2006}+\sqrt{2005}}=\frac{1}{\sqrt{2006}+\sqrt{2005}}\)
Tương tự cũng có: \(\frac{1}{\sqrt{2007}+\sqrt{2008}}\)
Dễ thấy: \(\sqrt{2005}+\sqrt{2006}< \sqrt{2007}+\sqrt{2008}\)
\(\Rightarrow\frac{1}{\sqrt{2006}+\sqrt{2005}}>\frac{1}{\sqrt{2007}+\sqrt{2008}}\)
Đúng 0
Bình luận (0)
So sánh \(\sqrt{2005}+\sqrt{2007}\) và \(2\sqrt{2006}\)
Ta có : \(\sqrt{2006}-\sqrt{2005}=\frac{1}{\sqrt{2006}+\sqrt{2005}}\)
\(\sqrt{2007}-\sqrt{2006}=\frac{1}{\sqrt{2007}+\sqrt{2006}}\)
Mà : \(\frac{1}{\sqrt{2006}+\sqrt{2005}}>\frac{1}{\sqrt{2007}-\sqrt{2006}}\)
Nến : \(\sqrt{2006}-\sqrt{2005}>\sqrt{2007}-\sqrt{2006}\)
\(\Rightarrow\sqrt{2005}+\sqrt{2007}< 2\sqrt{2006}\)
Đúng 0
Bình luận (0)
So sánh \(\sqrt{2005}+\sqrt{2007}\) và \(2\sqrt{2006}\)
\(\left(\sqrt{2005}+\sqrt{2007}\right)^2=4012+2\sqrt{2005.2007}\)
\(=4012+2\sqrt{\left(2016-1\right)\left(2016+1\right)}=4012+2\sqrt{2016^2-1}\)
\(\left(2\sqrt{2006}\right)^2=4012+4012=4012+2\sqrt{2016^2}\)
=>\(\left(\sqrt{2015}+\sqrt{2017}\right)^2< \left(2\sqrt{2016}\right)^2\Rightarrow\sqrt{2015}+\sqrt{2017}< 2\sqrt{2016}\)
Đúng 0
Bình luận (0)
Ta có: \(\sqrt{2006}-\sqrt{2005}=\frac{1}{\sqrt{2006}+\sqrt{2005}}\)
\(\sqrt{2007}-\sqrt{2006}=\frac{1}{\sqrt{2007}+\sqrt{2006}}\)
Mà: \(\frac{1}{\sqrt{2006}+\sqrt{2005}}>\frac{1}{\sqrt{2007}+\sqrt{2006}}\)
Nên: \(\sqrt{2006}-\sqrt{2005}>\sqrt{2007}-\sqrt{2006}\)
=>\(\sqrt{2005}+\sqrt{2007}< 2\sqrt{2006}\)
Đúng 0
Bình luận (0)
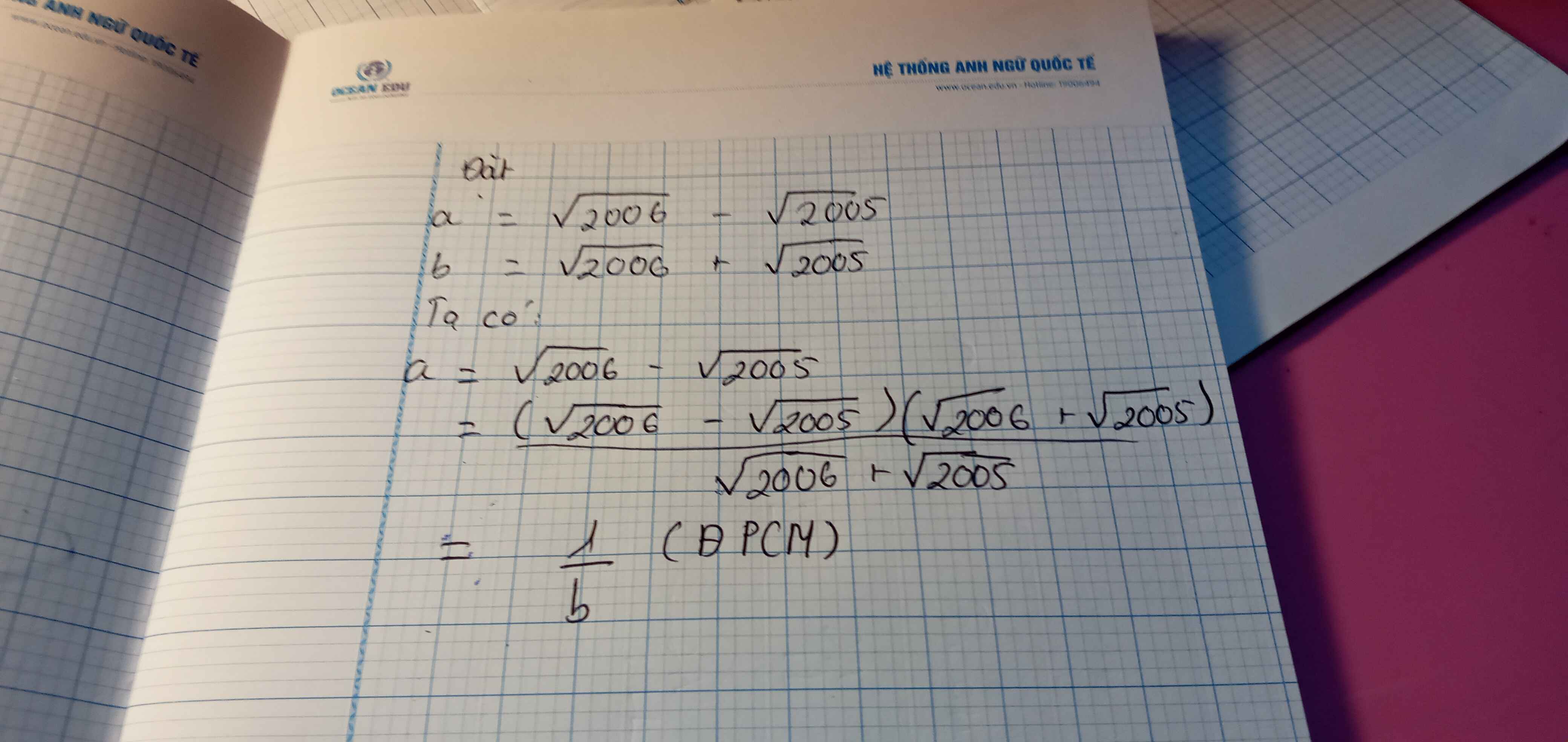
Chứng minh:
\(\left(\sqrt{2006}-\sqrt{2005}\right)\)và \(\left(\sqrt{2006}+\sqrt{2005}\right)\)là 2 số nghịch đảo của nhau.
Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)
Ta có
\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)
\(\RightarrowĐfcm\)
Đúng 6
Bình luận (1)
\(\sqrt{2006}-\sqrt{2005}=\dfrac{1}{\sqrt{2006}+\sqrt{2005}}\)
Do đó: \(\sqrt{2006}-\sqrt{2005};\sqrt{2006}+\sqrt{2005}\) là hai số nghịch đảo
Đúng 2
Bình luận (0)
So sánh :
\(\sqrt{2004}+\sqrt{2006}\) và \(2\sqrt{2005}\)
Giả sử : \(\sqrt{2004}+\sqrt{2006}< 2\sqrt{2005}\)
\(\Leftrightarrow2004+2006+2\sqrt{2004.2006}< 4.2005\)
\(\Leftrightarrow\sqrt{2004.2006}< 2005\Leftrightarrow2004.2006< 2005^2\)
\(\Leftrightarrow\left(2005-1\right)\left(2005+1\right)< 2005^2\)
\(\Leftrightarrow2005^2-1< 2005^2\) . BĐT đúng
Vậy \(\sqrt{2004}+\sqrt{2006}< 2\sqrt{2005}\)
Đúng 0
Bình luận (0)
Giả sử : \(\sqrt{2004}+\sqrt{2006}< 2\sqrt{2005}\)
\(\Leftrightarrow2004+2006+2\sqrt{2004.2006}< 4.2005\)
\(\Leftrightarrow\sqrt{2004.2006}< 2005\Leftrightarrow2004.2006< 2005^2\)
\(\Leftrightarrow\left(2005-1\right)\left(2005+1\right)< 2005^2\)
\(\Leftrightarrow2005^2-1< 2005^2.\) BĐT đúng
Vậy \(\sqrt{2004}+\sqrt{2006}< 2\sqrt{2005}\)
Đúng 0
Bình luận (0)
1/ So sánha) 3 - 2sqrt{3} và 2sqrt{6} - 5b) sqrt{4sqrt{5}} và sqrt{5sqrt{3}} c) 3 - 2sqrt{5} và 1 - sqrt{5} d) sqrt{2006} - sqrt{2005} và sqrt{2005} - sqrt{2004} e) sqrt{2003} + sqrt{2005} và 2sqrt{2004} 2/ Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất a) -x² + 4x - 2b) sqrt{2x^2:+:3} c) 2x - sqrt{1x} d) -3 + sqrt{2x^2:+:49} e) sqrt{9x^2:-:4x:+:65} f) -5 + sqrt{4:-:9x^2:+:6x}
Đọc tiếp
1/ So sánh
a) 3 - 2\(\sqrt{3}\) và 2\(\sqrt{6}\) - 5
b) \(\sqrt{4\sqrt{5}}\) và \(\sqrt{5\sqrt{3}}\)
c) 3 - 2\(\sqrt{5}\) và 1 - \(\sqrt{5}\)
d) \(\sqrt{2006}\) - \(\sqrt{2005}\) và \(\sqrt{2005}\) - \(\sqrt{2004}\)
e) \(\sqrt{2003}\) + \(\sqrt{2005}\) và \(2\sqrt{2004}\)
2/ Tìm giá trị nhỏ nhất hoặc giá trị lớn nhất
a) -x² + 4x - 2
b) \(\sqrt{2x^2\:+\:3}\)
c) 2x - \(\sqrt{1x}\)
d) -3 + \(\sqrt{2x^2\:+\:49}\)
e) \(\sqrt{9x^2\:-\:4x\:+\:65}\)
f) -5 + \(\sqrt{4\:-\:9x^2\:+\:6x}\)
2) \(-x^2+4x-2\)
\(=-\left(x^2-4x+2\right)\)
\(=-\left(x^2-4x+4-2\right)\)
\(=-\left(x-2\right)^2+2\)
Ta có: \(-\left(x-2\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-2\right)^2+2\le2\forall x\)
Dấu "=" xảy ra:
\(\Leftrightarrow-\left(x-2\right)^2+2=2\Leftrightarrow x=2\)
Vậy: GTLN của bt là 2 tại x=2
b) \(\sqrt{2x^2-3}\) (ĐK: \(x\ge\sqrt{\dfrac{3}{2}}\))
Mà: \(\sqrt{2x^2-3}\ge0\forall x\)
Dấu "=" xảy ra:
\(\sqrt{2x^2-3}=0\Leftrightarrow x=\sqrt{\dfrac{3}{2}}=\dfrac{3\sqrt{2}}{2}\)
Vậy GTNN của bt là 0 tại \(x=\dfrac{3\sqrt{2}}{2}\)
...
Đúng 0
Bình luận (0)
1:
b: \(4\sqrt{5}=\sqrt{80}\)
\(5\sqrt{3}=\sqrt{75}\)
=>\(4\sqrt{5}>5\sqrt{3}\)
=>\(\sqrt{4\sqrt{5}}>\sqrt{5\sqrt{3}}\)
c: \(3-2\sqrt{5}-1+\sqrt{5}=2-\sqrt{5}< 0\)
=>\(3-2\sqrt{5}< 1-\sqrt{5}\)
d: \(\sqrt{2006}-\sqrt{2005}=\dfrac{1}{\sqrt{2006}+\sqrt{2005}}\)
\(\sqrt{2005}-\sqrt{2004}=\dfrac{1}{\sqrt{2005}+\sqrt{2004}}\)
\(\sqrt{2006}+\sqrt{2005}>\sqrt{2005}+\sqrt{2004}\)
=>\(\dfrac{1}{\sqrt{2006}+\sqrt{2005}}< \dfrac{1}{\sqrt{2005}+\sqrt{2004}}\)
=>\(\sqrt{2006}-\sqrt{2005}< \sqrt{2005}-\sqrt{2004}\)
e: \(\left(\sqrt{2003}+\sqrt{2005}\right)^2=4008+2\cdot\sqrt{2003\cdot2005}=4008+2\cdot\sqrt{2004^2-1}\)
\(\left(2\sqrt{2004}\right)^2=4\cdot2004=4008+2\cdot\sqrt{2004^2}\)
=>\(\left(\sqrt{2003}+\sqrt{2005}\right)^2< \left(2\sqrt{2004}\right)^2\)
=>\(\sqrt{2003}+\sqrt{2005}< 2\sqrt{2004}\)
Đúng 0
Bình luận (0)