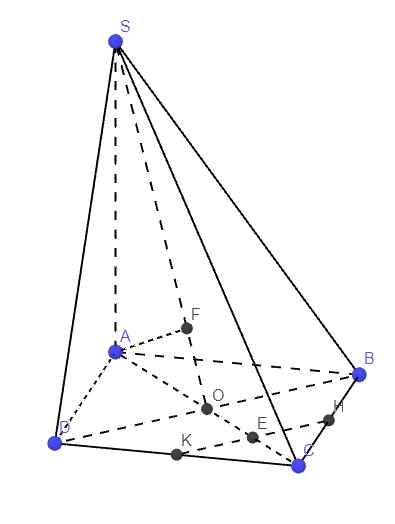
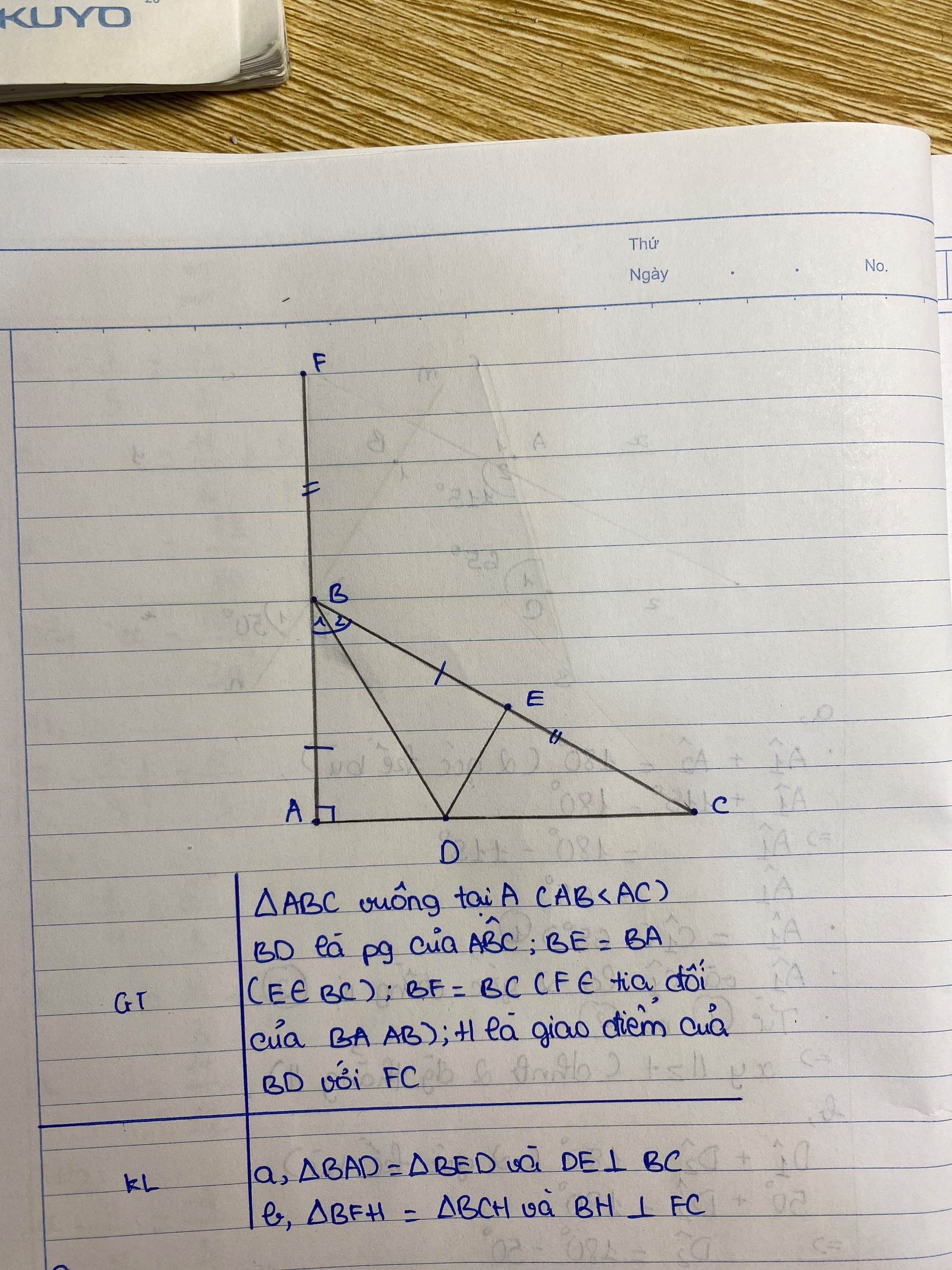
 giúp mình vẽ nốt hình và làm câu b ạ
giúp mình vẽ nốt hình và làm câu b ạ

Những câu hỏi liên quan
Giúp mình vẽ hình và làm câu b vs ạ
môn âm nhạc 7 ạ mong mn giúp!
câu 1.So sánh nhịp 2/4 và 3/4
câu 2.Vẽ sơ đồ hình nốt
Giống nhau:
-Đều có ô nhịp , phách, các nốt nhạc, giá trị của mỗi phách bằng nhau (1 phách)
Khác nhau:
-Nhịp 3/4 có 3 phách trong một ô nhịp
-Nhịp 3/4 là nhịp lẻ
-nhịp 2/4 có 2 phách trong một ô nhịp.
-nhịp 2/4 là nhịp chẵn.
Đúng 1
Bình luận (0)
 vẽ giúp mình hình và câu c,b với ạ, mình cảm ơn
vẽ giúp mình hình và câu c,b với ạ, mình cảm ơn

Ai giúp mình phần 2 nhỏ bài tìm gtri nguyên n với câu 3 bài hình đc ko ạ(kèm vẽ hình) nếu cần thiết mn làm giúp e câu 5 ạ ko thì thôi ạ. Mình cảm ơn nhiều
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
Đúng 2
Bình luận (0)
 Làm giúp mình câu a,b và vẽ hình
Làm giúp mình câu a,b và vẽ hình
a,b:
góc ACB=góc ADB=1/2*180=90 độ
=>CB vuông góc AM, BD vuông góc AN
ΔABN vuông tại B có BD vuông góc AN
nên AD*AN=AB^2
ΔABM vuông tại B có BC vuông góc AM
nên AC*AM=AB^2=AD*AN
=>AC/AN=AD/AM
=>ΔACD đồng dạng với ΔANM
=>góc ACD=góc ANM
=>góc DCM+goc DNM=180 độ
=>DNMC nội tiếp
Đúng 0
Bình luận (0)
Vẽ hình và làm a,b,c,d giúp mình nha cảm ơn ạ
a: Xét ΔBAE vuông tại A và ΔBIE vuông tại I có
BE chung
\(\widehat{ABE}=\widehat{IBE}\)
Do đó: ΔBAE=ΔBIE
Suy ra: BA=BI
hay ΔBIA cân tại B
b: Ta có: ΔBAE=ΔBIE
nên EA=EI
hay E nằm trên đường trung trực của AI(1)
Ta có: BA=BI
nên B nằm trên đường trung trực của AI(2)
Từ (1) và (2) suy ra BE là đường trung trực của AI
hay BE\(\perp\)AI
c: Xét ΔAEK vuông tại A và ΔIEC vuông tại I có
EA=EI
\(\widehat{AEK}=\widehat{IEC}\)
Do đó:ΔAEK=ΔIEC
Suy ra: AK=IC
Ta có: BA+AK=BK
BI+IC=BC
mà BA=BI
và AK=IC
nên BK=BC
hay ΔBKC cân tại B
d: Xét ΔBKC có BA/BK=BI/BC
nên AI//KC
Đúng 0
Bình luận (0)

Giúp em với ạ vẽ hình nữa làm mình câu a) cũng được ạ em cảm ơn nhìu ::)>>33
a.
Ta có \(BD||AC\) (cùng vuông góc AB)
Áp dụng định lý Talet trong tam giác ACE: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b.
Ta có \(IK||BD||AC\) \(\Rightarrow EI||AC\)
Áp dụng Talet: \(\dfrac{DC}{ED}=\dfrac{DA}{ID}\Rightarrow\dfrac{DC}{DC+ED}=\dfrac{DA}{DA+ID}\Rightarrow\dfrac{DC}{CE}=\dfrac{DA}{AI}\) (1)
Do \(BD||EK\), áp dụng Talet trong tam giác CEK: \(\dfrac{BD}{EK}=\dfrac{CD}{CE}\) (2)
Do \(BD||EI\), áp dụng Talet trong tam giác AEI: \(\dfrac{BD}{EI}=\dfrac{AD}{AI}\) (3)
Từ(1);(2);(3) \(\Rightarrow\dfrac{BD}{EK}=\dfrac{BD}{EI}\Rightarrow EK=EI\)
Đúng 2
Bình luận (0)
Giúp e vẽ hình và làm câu 34 đi ạ 

Gọi E là giao điểm HK và AC
\(\Rightarrow E\) là trung điểm OC \(\Rightarrow OE=\dfrac{1}{2}OC=\dfrac{1}{2}OA\)
\(\Rightarrow d\left(E;\left(SBD\right)\right)=\dfrac{1}{2}d\left(A;\left(SBD\right)\right)\)
HK là đường trung bình tam giác BCD \(\Rightarrow HK||BD\)
\(\Rightarrow d\left(HK;SD\right)=d\left(HK;\left(SBD\right)\right)=d\left(E;\left(SBD\right)\right)=\dfrac{1}{2}d\left(A;\left(SBD\right)\right)\)
Từ A kẻ \(AF\perp SO\Rightarrow AF\perp\left(SBD\right)\Rightarrow AF=d\left(A;\left(SBD\right)\right)\)
\(AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng:
\(AF=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{2a}{3}\)
\(\Rightarrow d\left(HK;SD\right)=\dfrac{1}{2}AF=\dfrac{a}{3}\)
Đúng 0
Bình luận (0)
Mọi người giải và vẽ hình giúp mình với ạ làm c11 thôi ạ
Bài 11:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và MN=AC/2(1)
Xét ΔCDA có
P là trung điểm của CD
Q là trung điểm của DA
Do đó: PQ là đường trung bình của ΔCDA
Suy ra: PQ//AC và PQ=AC/2(2)
Từ (1) và (2) suy raMN//PQ và MN=PQ
hay MNPQ là hình bình hành
Đúng 0
Bình luận (0)
giúp mình với ạ, vẽ hình, làm đầy đủ và chính xác 100% ạ