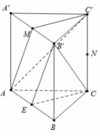
Cho lăng trụ ABC.A'B'C'. Gọi H là trung điểm A'B'. Tìm giao điểm của AC' và (BCH).
WS
Những câu hỏi liên quan
Cho lăng trụ ABC.A'B'C' có H là trung điểm của A'B'
a,C/m: CB' // (AHC')
b,:Tìm giao điểm của AC' vs mp (BCH)
c, (\(\alpha\)) đi qua CC' và song song với 2 đt AH,CB'
d, Xác định thiết diện của lăng trụ cắt bởi (\(\alpha\))
(a)đi pua cc" và song song với 2 đt AH,CB'
Đúng 0
Bình luận (0)
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi H là trung điểm của A'B'.
a) Chứng minh rằng CB′ // (AHC′)
b) Tìm giao tuyến d của (AB'C') và (ABC)
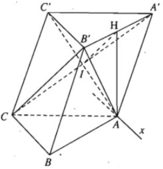
a) Ta có tứ giác AA’CC’ là hình bình hành suy ra A’C cắt AC’ tại trung điểm I của mỗi đường.
Do đó IH // CB′ ( đường trung bình của tam giác CB’A’)
Mặt khác IH ⊂ (AHC′) nên CB′ // (AHC′)
b) Ta có:
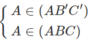
suy ra, ⇒ A là điểm chung của (AB’C’) và (ABC)
Mà
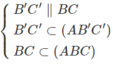
Nên (AB′C′) ∩ (ABC) = Ax
Và Ax // BC // B′C′
Đúng 0
Bình luận (0)
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi H là trung điểm củ A'B'
a) Chứng minh rằng CB'//A'I'
b) Tìm giao tuyến d của (AB'C') và (ABC)
Cho lăng trụ đều ABC.A'B'C' có AB = a và đường thẳng A'B tạo với đáy một góc bằng 60 độ. Gọi M và N lần lượt là trung điểm của các cạnh AC và B'C'. Tính theo a thể tích củ khối lăng trụ ABC.A'B'C' và độ dài của MN
\(AA'\perp\left(ABC\right)\Rightarrow\widehat{A'BA}\) là góc giữa A'B với đáy
Suy ra : \(\widehat{A'BA}=60^o\Rightarrow AA'=AB.\tan\widehat{A'BA}=a\sqrt{3}\)
Do đó \(V_{ABC.A'B'C'}=AA'.S_{\Delta ABC}=\frac{3a^2}{4}\)
Gọi K là trung điểm cạnh BC, suy ra Tam giác MNK vuông tại K, có :
\(MK=\frac{AB}{2}=\frac{a}{2};NK=AA'=a\sqrt{3}\)
Do đó : \(MN=\sqrt{MK^2+NK^2}=\frac{a\sqrt{13}}{2}\)
Đúng 0
Bình luận (0)
Cho hình lăng trụ ABC.A'B'C'. Gọi H là trung điểm của A'B'. Đường thẳng B'C song song với mặt phẳng nào sau đây?
A. (AHC')
B. (AA'H)
C. (HAB)
D. (HA'C')
Đáp án A
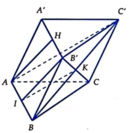
Gọi ![]() và I là trung điểm của AB
và I là trung điểm của AB
Do HB' = AI, HB'//AI => AHB'I là hình bình hành => AH//B'I
Mặt khác KI//AC' nên (AHC')//(B'CI)=> B'C//(AHC')
Đúng 0
Bình luận (0)
Cho hình lăng trụ ABC.A'B'C'. Gọi H là trung điểm của A'B'. Đường thẳng B'C song song với mặt phẳng nào sau đây?
A. (AHC')
B. (AA'H)
C. (HAB)
D. (HA'C')
Đáp án A.
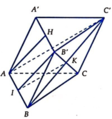
Gọi K = B ' C ∩ B C ' và I là trung điểm của AB
Do H B ' = A I , H B ' / / A I ⇒ A H B ' I là hình bình hành ⇒ A H / / B ' I
Mặt khác K I / / A C ' nên A H C ' / / B ' C I ⇒ B ' C / / A H C '
Đúng 0
Bình luận (0)
cho hình lăng trụ ABC.A'B'C' . gọi M,N lần lượt là trung điểm A'B' và AB CM:CB'//(AMC')
Cho lăng trụ
A
B
C
.
A
B
C
.
Gọi
M
,
N
lần lượt là trung điểm của
A
B
và
C
C
. Khi đó
C
B
song song với A. AM B.
B
C
M
C.
A...
Đọc tiếp
Cho lăng trụ A B C . A ' B ' C ' . Gọi M , N lần lượt là trung điểm của A ' B ' và C C ' . Khi đó C B ' song song với
A. AM
B. B C ' M
C. A ' N
D. A C ' M
Đáp án D
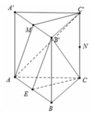
Gọi E là trung điểm của AB, ta có C E / / C ' M
Mặt khác A M / / E B ' do đó C ' M A / / B ' E C
Suy ra C B ' / / A C ' M
Đúng 0
Bình luận (0)
Cho lăng trụ ABC.A'B'C' Gọi M,N lần lượt là trung điểm của A'B' và CC' . Khi đó CB' song song với
A. AM
B. (BC'M)
C. A'N
D. (AC'M)
Cho lăng trụ ABC.ABC; M, N lần lượt là trung điểm AB và A’C’. Gọi V1, V2 là thể tích của hai phần lăng trụ bị chia ra bởi mặt phẳng (BCNM). Tính tỉ số
V
1
V
2
A.
V
1
V
2
5
7
B.
V
1...
Đọc tiếp
Cho lăng trụ ABC.A'B'C'; M, N lần lượt là trung điểm A'B' và A’C’. Gọi V1, V2 là thể tích của hai phần lăng trụ bị chia ra bởi mặt phẳng (BCNM). Tính tỉ số V 1 V 2
A. V 1 V 2 = 5 7
B. V 1 V 2 = 3 4
C. V 1 V 2 = 1
D. V 1 V 2 = 1 2
Đáp án A
Gọi ![]() => A’ là trung điểm AI
=> A’ là trung điểm AI
![]()
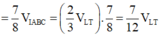
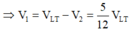
=> đáp án A
Đúng 0
Bình luận (0)