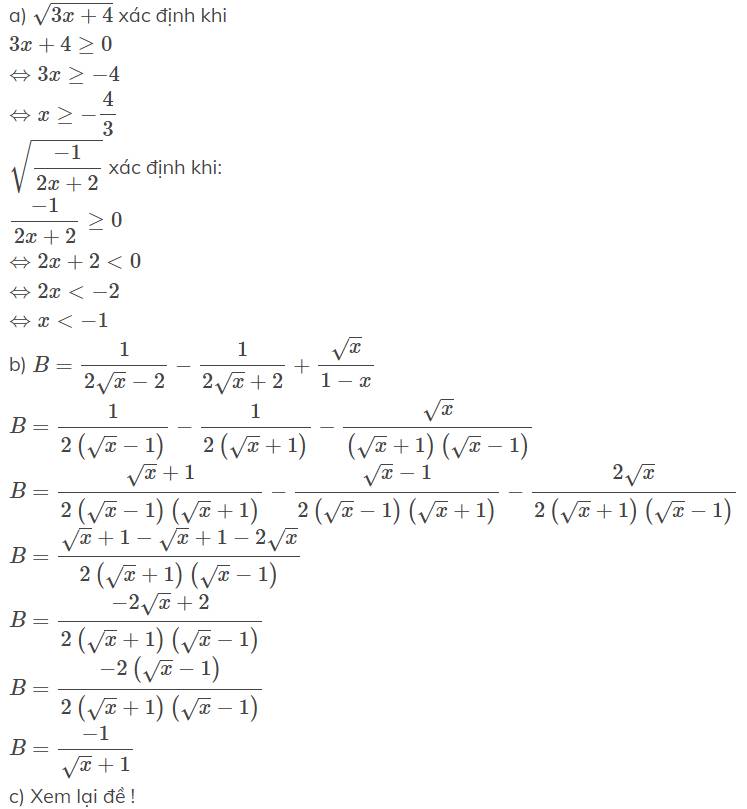Những biểu thức nào sau đây là đa thức: \(\sqrt{3x}-\dfrac{\sqrt{2}}{3}y\)\(+1\) ;\(xy+\dfrac{x}{y};\dfrac{\sqrt{x}+\sqrt{y}}{4};\dfrac{1}{x+y}\)\(;\left(\sqrt{5}-1\right)xy^2z\)
H24
Những câu hỏi liên quan
Biểu thức nào sau đây không phải là đa thức
A. \(\sqrt 2 {x^2}y\)
B. \( - \dfrac{1}{2}x{y^2} + 1\)
C. \(\dfrac{1}{{2z}}x + y\)
D. 0
Các biểu thức không phải đa thức là:
\(\sqrt{2}x^2y,0\)
Đúng 1
Bình luận (0)
Trong các biểu thức sau, biểu thức nào là đa thức?
\( - {x^2} + 3x + 1;\dfrac{x}{{\sqrt 5 }};x - \dfrac{{\sqrt 5 }}{x};2024;3{x^2}{y^2} - 5{x^3}y + 2,4;\dfrac{1}{{{x^2} + x + 1}}.\)
Các đa thức là: \( - {x^2} + 3x + 1;\dfrac{x}{{\sqrt 5 }};2024;3{x^2}{y^2} - 5{x^3}y + 2,4.\)
Đúng 0
Bình luận (0)
Trong các biểu thức sau, biểu thức nào là các phân thức?
\(\dfrac{{3x + 1}}{{2x - 1}}\) ; \(2{x^2} - 5x + 3\) ; \(\dfrac{{x + \sqrt x }}{{3x + 2}}\)
Các phân thức:
\(\dfrac{3x+1}{2x-1};\dfrac{x+\sqrt{x}}{3x+2}\)
Đúng 1
Bình luận (0)
BT2: Trong các biểu thức sau, biểu thức nào là đơn thức?
\(\left(1-\dfrac{1}{\sqrt{3}}\right)x^2,\dfrac{1}{2}\left(x^2-1\right),\dfrac{x^2.7}{2},6\sqrt{y},\dfrac{1-\sqrt{5}}{x},\dfrac{x-y^2}{4}\)
a) Với giá trị nào của x thì các biểu thức sau đây xác định :sqrt{3x+4} sqrt{dfrac{-1}{2x+2}}b) Rút gọn biểu thức B dfrac{1}{2sqrt{x}-2}-dfrac{1}{2sqrt{x}+2}+dfrac{sqrt{x}}{1-x} với x ≥ 0 , x ≠ 1c) Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nguyênD dfrac{2sqrt{x-1}}{sqrt{x}+3}
Đọc tiếp
a) Với giá trị nào của x thì các biểu thức sau đây xác định :
\(\sqrt{3x+4}\) \(\sqrt{\dfrac{-1}{2x+2}}\)
b) Rút gọn biểu thức B = \(\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}+\dfrac{\sqrt{x}}{1-x}\) với x ≥ 0 , x ≠ 1
c) Tìm các giá trị nguyên của x để các biểu thức sau có giá trị nguyên
D = \(\dfrac{2\sqrt{x-1}}{\sqrt{x}+3}\)
Biểu thức nào sau đây không phải là phân thức?
A. \({x^2}y + y\)
B. \(\dfrac{{3xy}}{{\sqrt 2 z}}\)
C. \(\dfrac{{\sqrt x }}{2}\)
D. \(\dfrac{{a + b}}{{a - b}}\)
Biểu thức không phải phân thức:
\(x^2y+y\)
⇒ Chọn A
Đúng 1
Bình luận (0)
bài 1: tìm điều kiện xác định với giá trị nào của x thì các biểu thức sau đây xác định
a, \(\sqrt{-2x+3}\)
b, \(\sqrt{3x+4}\)
c, \(\sqrt{1+x\overset{2}{ }}\)
d, \(\sqrt{^{-3}_{3x+5}}\)
e, \(\sqrt{\dfrac{2}{x}}\)
help me :((
a/ ĐKXĐ : \(-2x+3\ge0\)
\(\Leftrightarrow x\le\dfrac{3}{2}\)
b/ ĐKXĐ : \(3x+4\ge0\)
\(\Leftrightarrow x\ge-\dfrac{4}{3}\)
c/ Căn thức \(\sqrt{1+x^2}\) luôn được xác định với mọi x
d/ ĐKXĐ : \(-\dfrac{3}{3x+5}\ge0\)
\(\Leftrightarrow3x+5< 0\)
\(\Leftrightarrow x< -\dfrac{5}{3}\)
e/ ĐKXĐ : \(\dfrac{2}{x}\ge0\Leftrightarrow x>0\)
P.s : không chắc lắm á!
Đúng 2
Bình luận (0)
Biểu thức nào dưới đây là đa thức? Hãy chỉ rõ các hạng tử của mỗi đa thức ấy.
\(3x{y^2} - 1;x + \dfrac{1}{x};\sqrt 2 x + \sqrt 3 y;x + \sqrt {xy} + y.\)
Các biểu thức là đa thức là: \(3x{y^2} - 1;\sqrt 2 x + \sqrt 3 y.\)
Đa thức \(3x{y^2} - 1\) có hai hạng tử là \(3x{y^2}\) và \( - 1\).
Đa thức \(\sqrt 2 x + \sqrt 3 y\) có hai hạng tử là \(\sqrt 2 x\) và \(\sqrt 3 y\).
Đúng 0
Bình luận (0)
Biểu thức nào sau đây là đa thức một biến?
a) \({x^2} + 9;\)
b) \(\dfrac{2}{{{x^2}}} + 2x + 1;\)
c) \(3x + \dfrac{2}{5}y.\)
a) \({x^2} + 9\) là đa thức một biến x.
b) \(\dfrac{2}{{{x^2}}} + 2x + 1\) không phải là đa thức một biến x.
c) \(3x + \dfrac{2}{5}y\) không phải là đa thức một biến x hay y.
Đúng 0
Bình luận (0)
Với giá trị nào của x thì mỗi căn thức sau đây có nghĩa:a) sqrt{dfrac{x}{3}}b) sqrt{-5x}c) sqrt{4-x}d) sqrt{3x+7}e) sqrt{-3x+4}f) sqrt{dfrac{1}{-1+x}}g) sqrt{1+x^2}h) sqrt{dfrac{5}{x-2}}
Đọc tiếp
Với giá trị nào của x thì mỗi căn thức sau đây có nghĩa:
a) \(\sqrt{\dfrac{x}{3}}\)
b) \(\sqrt{-5x}\)
c) \(\sqrt{4-x}\)
d) \(\sqrt{3x+7}\)
e) \(\sqrt{-3x+4}\)
f) \(\sqrt{\dfrac{1}{-1+x}}\)
g) \(\sqrt{1+x^2}\)
h) \(\sqrt{\dfrac{5}{x-2}}\)
a) Để \(\sqrt{\dfrac{x}{3}}\) có nghĩa thì \(\dfrac{x}{3}\ge0\Leftrightarrow x\ge0\)
b) Để \(\sqrt{-5x}\) có nghĩa thì \(-5x\ge0\Leftrightarrow x\le0\)
c) Để \(\sqrt{4-x}\) có nghĩa thì \(4-x\ge0\Leftrightarrow x\le4\)
d) Để \(\sqrt{3x+7}\) có nghĩa thì \(3x+7\ge0\Leftrightarrow x\ge-\dfrac{7}{3}\)
e) Để \(\sqrt{-3x+4}\) có nghĩa thì \(-3x+4\ge0\Leftrightarrow x\le\dfrac{4}{3}\)
f) Để \(\sqrt{\dfrac{1}{-1+x}}\) có nghĩa thì \(\left\{{}\begin{matrix}\dfrac{1}{-1+x}\ge0\\-1+x\ne0\end{matrix}\right.\)
\(\Leftrightarrow-1+x>0\Leftrightarrow x>1\)
g) Để \(\sqrt{1+x^2}\) có nghĩa thì \(1+x^2\ge0\left(đúng\forall x\right)\)
h) \(\sqrt{\dfrac{5}{x-2}}\) có nghĩ thì \(\left\{{}\begin{matrix}\dfrac{5}{x-2}\ge0\\x-2\ne0\end{matrix}\right.\)
\(\Leftrightarrow x-2>0\Leftrightarrow x>2\)
Đúng 2
Bình luận (1)
a. \(x\ge0\)
b. \(x< 0\)
c. \(x\le4\)
d. \(x\ge\dfrac{-7}{3}\)
e. \(x\le\dfrac{4}{3}\)
f. \(x>1\)
g. Mọi x
h. \(x>2\)
Đúng 0
Bình luận (0)