Giải bất pt sau: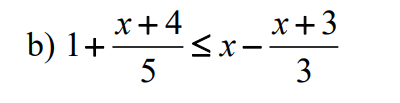

Những câu hỏi liên quan
Giải bất pt sau
\(\left(x-1\right)\left(3x^2+9x-12\right)< 0\)
Giải bất pt sau:
a, x^2 - 5x + 6 nhỏ hơn hoặc bằng 0
\(x^2-5x+6\le0\)
\(\Leftrightarrow x^2-2x-3x+6\le0\)
\(\Leftrightarrow x.\left(x-2\right)-3.\left(x-2\right)\le0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)\le0\)
\(\text{Mà }x-2>x-3\text{ nên :}\)
\(x-2\ge0\text{ và }x-3\le0\)
\(\Leftrightarrow x\ge2\text{ và }x\le3\Rightarrow2\le x\le3\)
Đúng 1
Bình luận (0)
M.n ơi giải giúp mìn bài 2 .3 câu giải bất pt và hệ bất pt vs tí nx mìn thi rồi .giúp mìn vs
\(\left\{{}\begin{matrix}3x+1< x-7\\1-2x>x+1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x< -8\\3x< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< -4\\x< 0\end{matrix}\right.\) \(\Rightarrow x< -4\)
Vậy nghiệm của hệ là \(S=\left(-\infty;-4\right)\)
Đúng 0
Bình luận (0)
Giải hệ bất pt sau :
\(\left\{{}\begin{matrix}4-3x-x^2\ge0\\x^2+x-2>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-4\le x\le1\\\left[{}\begin{matrix}x>1\\x< -2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow-4\le x< -2\)
Đúng 0
Bình luận (0)
áp dụng bất đẳng thức giải pt sau
\(6\sqrt[3]{x^3+2x^2+2x+2}=x^2+9x+19\)
giải pt và bất pt sau:
a.5|2x-1|-3=7
b.(2x+3)(x-2)-x^2+4=0
c. 2x-3/2<1-3x/-5
a, \(5\left|2x-1\right|-3=7\Leftrightarrow5\left|2x-1\right|=10\Leftrightarrow\left|2x-1\right|=2\)
TH1 : \(2x-1=2\Leftrightarrow x=\frac{3}{2}\)
TH2 : \(2x-1=-2\Leftrightarrow x=-\frac{1}{2}\)
b, \(\left(2x+3\right)\left(x-2\right)-x^2+4=0\Leftrightarrow\left(2x+3\right)\left(x-2\right)-\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x+3-x-2\right)=0\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\Leftrightarrow x=-1;x=2\)
c, \(\frac{2x-3}{2}< \frac{1-3x}{-5}\Leftrightarrow\frac{2x-3}{2}+\frac{1-3x}{5}< 0\)
\(\Leftrightarrow\frac{10x-15+2-6x}{10}< 0\Rightarrow4x-13< 0\Leftrightarrow x< \frac{13}{4}\)
`1.` giải pt :
`a)|-7x|=3x+16`
`b)(x-1)/(x+2)-x/(x-2)=(5x-8)/(x^2-4)`
`2.` giải bất phương trình sau và biểu diễn nghiệm trên trục số
`7x+5<3x-11`
1.a)|−7x|=3x+16
Vì |-7x| ≥ 0 nên 3x+16 ≥ 0 ⇔ x ≥ \(\dfrac{-16}{3}\) (*)
Với đk (*), ta có: |-7x|=3x+16
\(\left[\begin{array}{} -7x=3x+16\\ -7x=-3x-16 \end{array} \right.\) ⇔ \(\left[\begin{array}{} -7x-3x=16\\ -7x+3x=-16 \end{array} \right.\)
⇔ \(\left[\begin{array}{} x=-1,6 (t/m)\\ x= 4 (t/m) \end{array} \right.\)
b) \(\dfrac{x-1}{x+2}\) - \(\dfrac{x}{x-2}\) = \(\dfrac{5x-8}{x^2-4}\)
⇔ \(\dfrac{(x-1)(x-2)}{x^2-4}\) - \(\dfrac{x(x+2)}{x^2-4}\) = \(\dfrac{5x-8}{x^2-4}\)
⇒ x2 - 2x - x + 2 - x2 - 2x = 5x - 8
⇔ -5x - 5x = -8 - 2
⇔ -10x = -10
⇔ x=1
2.7x+5 < 3x−11
⇔ 7x - 3x < -11 - 5
⇔ 4x < -16
⇔ x < -4
bạn tự biểu diễn trên trục số nha !
Đúng 1
Bình luận (0)
GIẢI BẤT PT SAU VÀ BIỂU DIỄN TẬP HỢP NGHIỆM TRÊN TRỤC SỐ:
\(\text{7x + 4 ≥ 5x - 8 }\)
Lời giải:
$7x+4\geq 5x-8$
$\Leftrightarrow 2x\geq -12$
$\Leftrightarrow x\geq -6$

giải bất pt sau:
\(\frac{\sqrt{x^{2^{ }}-x-2}}{\sqrt{x-1}}+\sqrt{x-1}< \frac{2x+1}{\sqrt{x-1}}\)
Dk 1<x<2
√x^2 -x -2<x+2
5x+6>0
X > -6/5
Bpt vô nghiệm
Đúng 0
Bình luận (0)
\(7\left(2x-4\right)>1-4x\) giải bất pt
\(7\left(2x-4\right)>1-4x\)
\(\Leftrightarrow14x-28-1+4x>0\)
\(\Leftrightarrow x>\dfrac{29}{18}\)
Đúng 1
Bình luận (1)








