Viết phương trình tham số và phương trình chính tắc của đường thẳng MN, biết M(2; 0; −1) và N(4; 3; 1).
H24
Những câu hỏi liên quan
Viết phương trình tham số và phương trình chính tắc của đường thẳng (d): x + y - 20 = 0
\(\left(d\right):x+y-20=0.\\ \Rightarrow\overrightarrow{n_d}=\left(1;1\right).\\ \Rightarrow\overrightarrow{u_d}=\left(1;-1\right).\)
\(Cho\) \(x=1.\Rightarrow y=19.\Rightarrow A\left(1;19\right)\in\left(d\right).\)
Ta có \(\left(d\right):\) đi qua \(A\left(1;19\right);\overrightarrow{u_d=}\left(1;-1\right)\) là vecto chỉ phương.
\(\Rightarrow\) Phương trình tham số:
\(\left\{{}\begin{matrix}y=1+t.\\y=19-t.\end{matrix}\right.\)
\(\Rightarrow\) Phương trình chính tắc:
\(\dfrac{x-1}{1}=\dfrac{y-19}{-1}.\\ \Leftrightarrow x-1=-y+19.\)
Đúng 1
Bình luận (1)
(d):x+y−20=0.⇒→nd=(1;1).⇒→ud=(1;−1).(d):x+y−20=0.⇒nd→=(1;1).⇒ud→=(1;−1).
ChoCho x=1.⇒y=19.⇒A(1;19)∈(d).x=1.⇒y=19.⇒A(1;19)∈(d).
Ta có (d):(d): đi qua A(1;19);−−−→ud=(1;−1)A(1;19);ud=→(1;−1) là vecto chỉ phương.
⇒⇒ Phương trình tham số:
{y=1+t.y=19−t.{y=1+t.y=19−t.
⇒⇒ Phương trình chính tắc:
HT
Đúng 0
Bình luận (0)
Viết phương trình tham số, phương trình chính tắc của đường thẳng ∆ trong các trường hợp sau: ∆ đi qua hai điểm C(1; -1; 1) và D(2; 1; 4)
∆ đi qua hai điểm C và D nên có vecto chỉ phương CD → = (1; 2; 3)
Vậy phương trình tham số của ∆ là
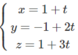
Phương trình chính tắc của ∆ là:
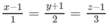
Đúng 0
Bình luận (0)
Viết phương trình tham số, phương trình chính tắc của đường thẳng ∆ trong các trường hợp sau: ∆ đi qua điểm A(1; 2; 3) và có vecto chỉ phương a → = (3; 3; 1)
Phương trình tham số của đường thẳng Δ đi qua điểm A(1; 2; 3) và có vecto chỉ phương
a
→
= (3; 3; 1) là: 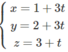
Phương trình chính tắc của ∆ là:
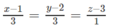
Đúng 0
Bình luận (0)
Viết phương trình tham số, phương trình chính tắc của đường thẳng ∆ trong các trường hợp sau: ∆ đi qua điểm B(1; 0; -1) và vuông góc với mặt phẳng ( α ) : 2x – y + z + 9 = 0
∆ ⊥ ( α ) ⇒ a ∆ → = a α → = (2; −1; 1)
Phương trình tham số của ∆ là
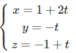
Phương trình chính tắc của ∆ là:
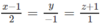
Đúng 0
Bình luận (0)
Đường thẳng d có phương trình chính tắc
x
+
1
-
3
y
-
2
1
.Phương trình nào sau đây là phương trình tham số của d?
Đọc tiếp
Đường thẳng d có phương trình chính tắc x + 1 - 3 = y - 2 1 .Phương trình nào sau đây là phương trình tham số của d?
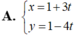

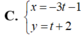
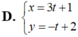
Đường thẳng d có ![]() và đi qua điểm M(-1; 2)
và đi qua điểm M(-1; 2)
Vậy phương trình tham số của đường thẳng 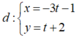 .
.
Chọn C.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số
x
2
+
t
y
-
3
t
z
-
1
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số x = 2 + t y = - 3 t z = - 1 + 5 t . Phương trình chính tắc của đường thẳng d là?
A. x - 2 = y = z + 1
B. x - 2 1 = y - 3 = z + 1 5
C. x + 2 - 1 = y 3 = z - 1 - 5
D. x + 2 1 = y - 3 = z - 1 5
Chọn B.
Đường thẳng d đi qua điểm A(2;0;-1) và có vectơ chỉ phương ![]()
Vậy phương trình chính tắc của d là x - 2 1 = y - 3 = z + 1 5
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số
x
2
+
t
y
3
-
t
z
-
1
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình tham số x = 2 + t y = 3 - t z = - 1 + 5 t . Phương trình chính tắc của đường thẳng d là?
A. x - 2 = y = z + 1
B. x - 2 1 = y - 3 = z + 1 5
C. x + 2 - 1 = y 3 = z - 1 - 5
D. x + 2 1 = y - 3 = z - 1 5
Chọn B.
Đường thẳng d đi qua điểm A(2;0;-1) và có vectơ chỉ phương ![]()
Vậy phương trình chính tắc của d là x - 2 1 = y - 3 = z + 1 5
Đúng 0
Bình luận (0)
Viết phương trình chính tắc của đường thẳng D đi qua M( -2; -1) và nhận vectơ
u
→
(
1
;
2
)
làm vectơ chỉ phương. A. 2x- y+ 3 0 B.
x
+
2
1
y
+
1
2...
Đọc tiếp
Viết phương trình chính tắc của đường thẳng D đi qua M( -2; -1) và nhận vectơ u → ( 1 ; 2 ) làm vectơ chỉ phương.
A. 2x- y+ 3= 0
B. x + 2 1 = y + 1 2
C. x = - 2 + 1 t y = - 1 + 2 t
D: x - 1 - 2 = y - 2 - 1
cho tam giác ABC có A(-1;2), B(-2;-1) và C(3;-2)a) Viết phương trình tham số của đường thẳng đi qua cạnh ACb) Viết phương trình tham số của đường trung tuyến BNc) Viết phương trình tham số của đường cao AHd) Viết phương trình tham số của đường trung trực đoạn ABe) Viết phương trình tham số của đường thẳng qua A và song song BCf) Viết phương trình tham số của đường thẳng đi qua M(3;-1) và vuông góc với OBg) Viết phương trình tham số của đường thẳng đi qua A và song song với(d): left{{}begin{matri...
Đọc tiếp
cho tam giác ABC có A(-1;2), B(-2;-1) và C(3;-2)
a) Viết phương trình tham số của đường thẳng đi qua cạnh AC
b) Viết phương trình tham số của đường trung tuyến BN
c) Viết phương trình tham số của đường cao AH
d) Viết phương trình tham số của đường trung trực đoạn AB
e) Viết phương trình tham số của đường thẳng qua A và song song BC
f) Viết phương trình tham số của đường thẳng đi qua M(3;-1) và vuông góc với OB
g) Viết phương trình tham số của đường thẳng đi qua A và song song với
(d): \(\left\{{}\begin{matrix}x=2-5t\\y=1+2t\end{matrix}\right.\)
a: vecto AC=(4;-4)=(1;-1)
Phương trìh tham số là:
x=-1+t và y=2-t
b: Tọa độ N là:
\(\left\{{}\begin{matrix}x=\dfrac{-1+3}{2}=\dfrac{2}{2}=1\\y=\dfrac{2-2}{2}=0\end{matrix}\right.\)
N(1;0); B(-2;-1)
vecto BN=(3;1)
Phương trình tham số là:
x=1+3t và y=0+t=t
c: vecto BC=(5;-1)
=>vecto AH=(1;5)
Phương trình tham số AH là:
x=-1+t và y=2+5t
Đúng 1
Bình luận (0)
Bài tập 1: Cho đường thẳng đi qua điểm và có vectơ pháp tuyến . Viết phương trình tham số và phương trình tổng quát của đường thẳng .Bài tập 2: Cho tam giác ABC có . a) Viết phương trình tổng quát của cạnh BC. b) Viết phương trình tham số của đường t...
Xem chi tiết





