các bạn giải theo kiểu tự luận giúp mik ;-;




Những câu hỏi liên quan
Giải giúp mk theo kiểu tự luận
Viết liên tiếp các số tự nhiên 12345... để được số có 378 chữ số. Hỏi số đó chia 5 dư bao
nhiêu? giúp mik nhé, giải tự luận giúp mik, mik cảm ơn các bạn(hạn trước thứ 4)
Đặt các số 1;2;3;4;5 vào các vòng tròn để tổng ba số theo hàng dọc hoặc theo hàng ngang đều bằng 9.
Mik giải ra rùi nhưng ko biết có đúng hay ko?các bạn chờ ở bình luận và nhận xét giúp mik nhé.
Tổng của ba số theo hàng dọc và ba số theo hàng ngang là:9+9=18
Tổng của năm số trong hình vẽ là:1+2+3+4+5=15
Chênh lệch :18-15=3
Sở dĩ chênh lệch là vì số ở giữa được tính nhiều lần hơn các số kia vì thế số ở giữa là 3.
Tổng của hai số đầu bằng:9-3=6
Do 1+5=2+4=6 nên các số sẽ được xếp như hình tám.
Đúng 0
Bình luận (0)
Đúng thì k cho mik còn sai thì sửa lại giúp mik cảm ơn nhìu
Đúng 0
Bình luận (0)
Sắp xếp các phân số theo thứ tự từ nhỏ đến lớn: − 19 /30 ; − 5/ 9 ; 0 ; − 25/ 47 ; 124/ 2011 ; − 24/ 35 ; − 23 /49 . giúp mik với các bạn giải thích từng bước giải giúp mik nhé!
\(\dfrac{-24}{35}< \dfrac{-19}{30}< \dfrac{-5}{9}< \dfrac{-25}{47}< \dfrac{-23}{49}< 0< \dfrac{124}{2011}\)
Đúng 0
Bình luận (0)


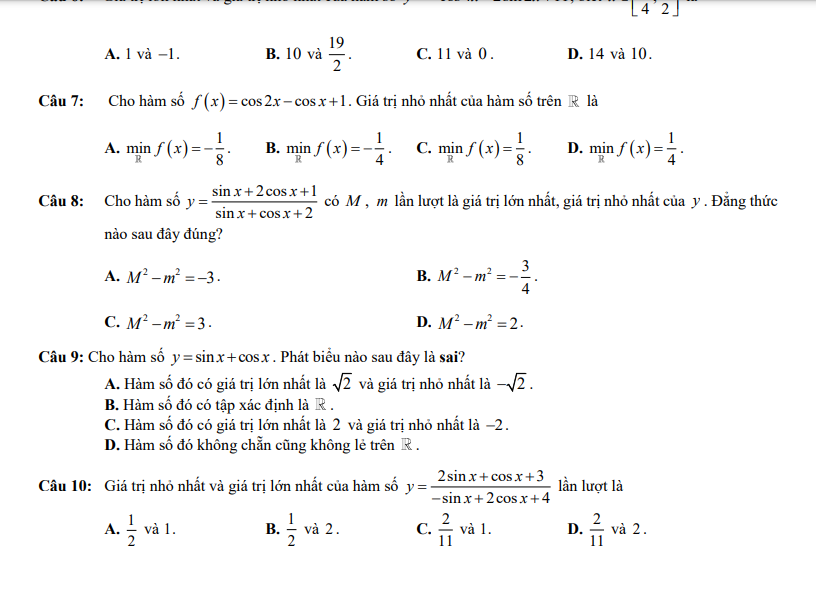
giải giùm em theo kiểu tự luận ạ
1.
\(2sinx+cosx=4\)
\(\Leftrightarrow\sqrt{5}\left(\dfrac{2}{\sqrt{5}}sinx+\dfrac{1}{\sqrt{5}}cosx\right)=4\)
\(\Leftrightarrow sin\left(x+arccos\dfrac{2}{\sqrt{5}}\right)=\dfrac{4}{\sqrt{5}}>1\)
\(\Rightarrow2sinx+4cosx-4\ne0\)
Khi đó:
\(2P.sinx+P.cosx-4P=sinx-2cosx-3\)
\(\Leftrightarrow\left(2P-1\right)sinx+\left(P+2\right)cosx=4P-3\)
Phương trình có nghiệm khi:
\(\left(2P-1\right)^2+\left(P+2\right)^2\ge\left(4P-3\right)^2\)
\(\Leftrightarrow4P^2-4P+1+P^2+4P+4\ge16P^2+9-24P\)
\(\Leftrightarrow11P^2-24P+4\le0\)
\(\Leftrightarrow\dfrac{2}{11}\le P\le2\)
\(\Rightarrow maxP=2\)
Đúng 2
Bình luận (0)
Tìm x
( 3 . x -12 ) . ( 8 - x ) = 0
Giải theo kiểu lý luận nha các bạn
=>3x-12=0 hoặc 8-x=0
=>x=4 hoặc x=8
Đúng 0
Bình luận (0)
Các bn giải chi tiết giúp mik bài này theo kiểu lớp 7 với.Cần gấppp
a) \(\left(x-\dfrac{1}{3}\right)^2=\dfrac{4}{9}\)
⇔ \(\left[{}\begin{matrix}x-\dfrac{1}{3}=\dfrac{2}{3}\\x-\dfrac{1}{3}=-\dfrac{2}{3}\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
d: \(\Leftrightarrow x^3=-8\)
hay x=-2
Đúng 0
Bình luận (0)
viết 1 đoạn văn 7 đến 8 câu theo kiểu diễn dịch làm sáng tỏ luận điểm ''Đại La là thánh địa xứng của đế vương muôn đời'' giúp mik giải nhé
chứng minh rằng :
+Lịch sử : Bề dày lịch sử là kinh đo cũ của cao vương tức là đã có sự trải nghiệm
+địa lý : trung tâm trời đất đc thế rồng cuộn hổ ngồi chính ngôi nam bắc đông tây tiện hướng nhìn sông dựa núi .
=> thế đất giàu tiềm năng thu hút đc nhiều nguồn năng lượng tự nhiên thuận lợi tự nhiên thuận lợi cho sự phát triển sinh tồn của vạn vật
+về kinh tế :đại thế đất rộng mà bằng đất đai cao mà thoáng muôn vật sẽ đc phong phú tốt tươi an cư lập nghiệp ko phải chịu cảnh khốn khổ ngập lụt +về chính trị , an ninh , quốc phòng
nơi này là thắng địa ,chốn hội tụ trọng yếu của 4 phương đất nước .kinh đô bậc nhất của đế vương muôn đời
xét toàn diện thì thành đại la xứng đáng là kinh đô bậc nhất không nơi nào sánh được
Đúng 1
Bình luận (0)
TÌM X
( Y+2) + ( Y+4)+........+(Y+1994)=997000
Các bạn giải tự luận giúp mik nha
Gấp lắm rồi
Cảm ơn các bạn
( Y+2) + ( Y+4)+........+(Y+1994)=997000
(Y + Y + .... + Y ) + (2 + 4 + ... + 1994 ) = 997000
Y x 997 + [ (1994 + 2 ) x 997 : 2 ] = 997000
Y x 997 + 995 006 = 997000
Y x 997 = 997000 - 995 006
Y x 997 = 1994
Y = 1994 : 997
Y = 2.
Vậy Y = 2.
Hok tốt !
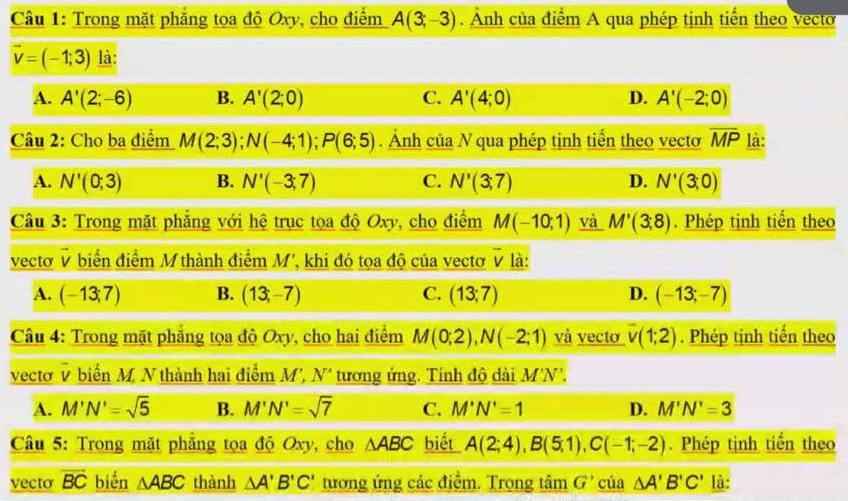
mọi người làm giúp em theo kiểu tự luận với ạ
1.
\(\left\{{}\begin{matrix}x_{A'}=x_A+\left(-1\right)=2\\y_{A'}=y_A+3=0\end{matrix}\right.\) \(\Rightarrow A'\left(2;0\right)\)
2.
\(\overrightarrow{MP}=\left(4;2\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{N'}=x_N+4=-4+4=0\\y_{N'}=y_N+2=1+2=3\end{matrix}\right.\)
\(\Rightarrow N'\left(0;3\right)\)
3.
\(\overrightarrow{MM'}=\left(13;7\right)\Rightarrow\overrightarrow{v}=\overrightarrow{MM'}=\left(13;7\right)\)
4.
\(\overrightarrow{MN}=\left(-2;-1\right)\Rightarrow MN=\sqrt{\left(-2\right)^2+\left(-1\right)^2}=\sqrt{5}\)
\(\Rightarrow M'N'=MN=\sqrt{5}\)
5.
Gọi G là trọng tâm ABC \(\Rightarrow G\left(2;1\right)\)
\(\overrightarrow{BC}=\left(-6;-3\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x_{G'}=2-6=-4\\y_{G'}=1-3=-2\end{matrix}\right.\) \(\Rightarrow G'\left(-4;-2\right)\)
Đúng 1
Bình luận (0)





