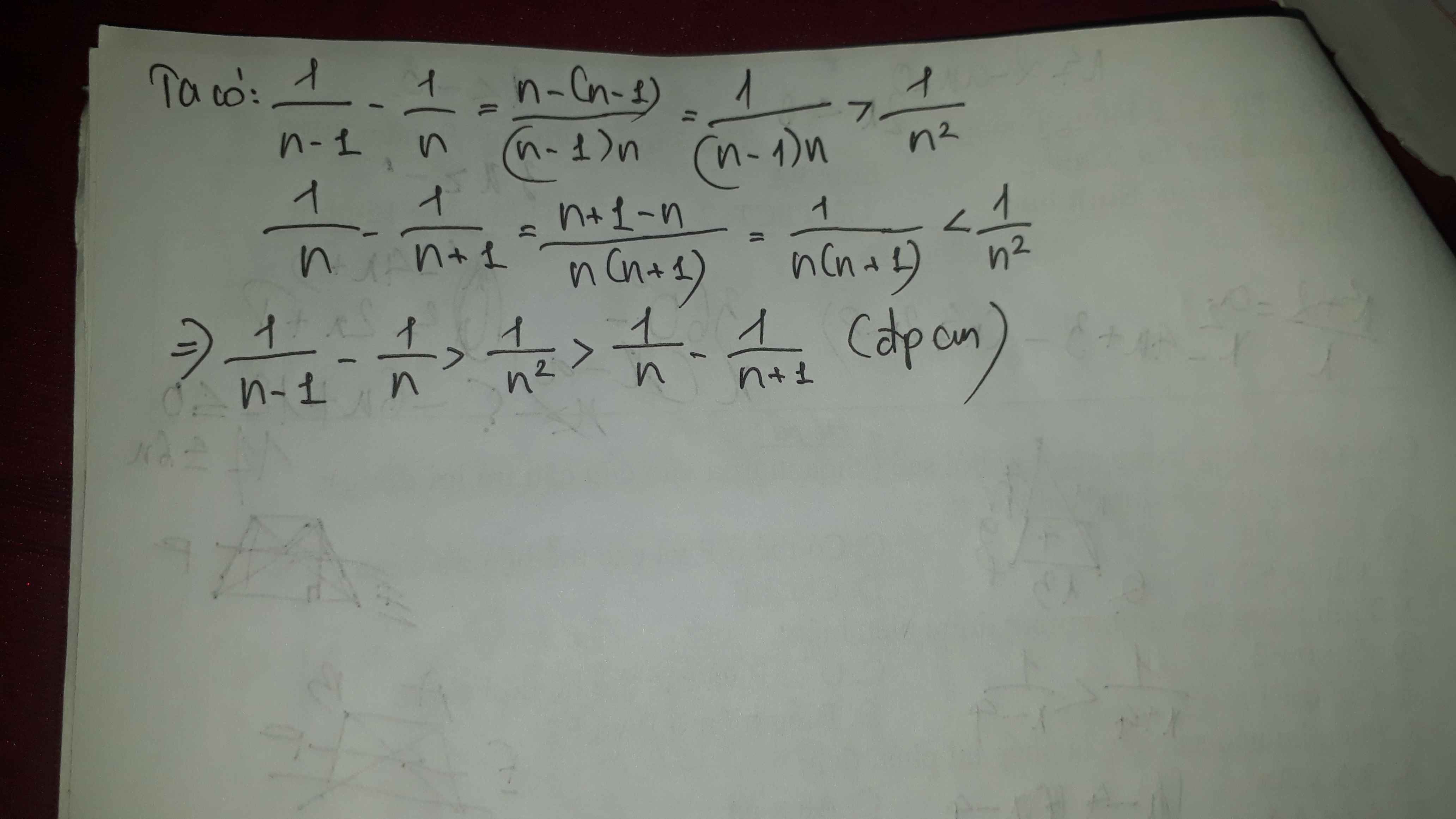chứng minh: \(\dfrac{n^5}{5}+\dfrac{n^3}{3}+\dfrac{7n}{15}\) \(\in Z\)với \(\forall n\in Z\)
NT
Những câu hỏi liên quan
chứng minh: \(\dfrac{n^5}{5}+\dfrac{n^3}{3}+\dfrac{7n}{15}\) \(\in Z\)với \(\forall n\in Z\)
chứng minh \(\dfrac{n}{12}+\dfrac{n^2}{8}+\dfrac{n^3}{24}\in Z\) với\(\forall n=2k\)
\(\dfrac{n}{12}+\dfrac{n^2}{8}+\dfrac{n^3}{24}\)
\(=\dfrac{n^3+3n^2+2n}{24}=\dfrac{n\left(n+1\right)\left(n+2\right)}{24}\)
Ta có: \(n\left(n+1\right)\left(n+2\right)\) là tích 3 số nguyên liên tiếp nên chia hết cho 3.
Vì \(n=2k\) nên suy ra n và (n + 2) là 2 số chẵn liên tiếp nên sẽ có 1 số chia hết cho 2, 1 số chia hết cho 4.
\(\Rightarrow n\left(n+1\right)\left(n+2\right)⋮8\)
Vì 3 và 8 nguyên tố cùng nhau nên: \(\Rightarrow n\left(n+1\right)\left(n+2\right)⋮24\)
Vậy ta có ĐPCM
Đúng 0
Bình luận (0)
a)cmr:
\(\dfrac{n^5}{5}=\dfrac{n^3}{3}=\dfrac{7n}{15}\) là số nguyên với mọi n \(\in Z\)
b)cmr:với n chẵn thì \(\dfrac{n}{12}+\dfrac{n^2}{8}+\dfrac{n^3}{24}\) là số nguyên
\(\frac{a^5}{5}+\frac{a^3}{3}+\frac{7a}{15}\left(n\Rightarrow a\text{ }nha\right)=\frac{a^5}{5}+\frac{a^3}{3}+\frac{7a}{15}=\frac{a^5}{5}+\frac{a^3}{3}+\frac{15a-5a-3a}{15}=\frac{a^5-a}{5}+\frac{a^3-a}{3}+\frac{15a}{15}=\frac{a^5-a}{5}+\frac{a^3-a}{3}+a;a^k-a⋮k\left(a\in Z;1< k\in N\right)\left(fecmat\right)\Rightarrow\left\{{}\begin{matrix}a^5-a⋮5\\a^3-a⋮3\end{matrix}\right.\Rightarrow dpcm\)
Đúng 0
Bình luận (0)
\(\frac{a}{12}+\frac{a^2}{8}+\frac{a^3}{24}\left(n\Rightarrow a\text{ nha}\right)=\frac{a^3+3a^2+2a}{24}=\frac{\left(a+2\right)\left(a+1\right)a}{24}.a=2k\left(k\in N\right)\Rightarrow;\frac{a\left(a+1\right)\left(a+2\right)}{24}=\frac{2k.\left(2k+1\right)\left(2k+2\right)}{24}=\frac{k\left(k+1\right)\left(2k+1\right)}{6}\Leftrightarrow k\left(k+1\right)\left(2k+1\right)⋮6\)
Đúng 1
Bình luận (0)
CMR \(A=\dfrac{n^3}{3}+\dfrac{n^5}{5}+\dfrac{7n}{15}\)ϵ Z với nϵZ
Sam Tiểu Thư bn đăng câu hỏi sai nơi rồi nha
Đúng 0
Bình luận (0)
CMR nếu n ∈ Z thì \(\dfrac{n^5}{5}+\dfrac{n^3}{3}+\dfrac{7n}{15}\) là số nguyên
1: \(\dfrac{\left(2^{12}\cdot3^5-4^6\cdot9^2\right)}{\left(2^2\cdot3\right)^6+8^4\cdot3^5}-\dfrac{\left(5^{10}\cdot7^3-25^5\cdot49^2\right)}{\left(125\cdot7\right)^3-5^9\cdot14^3}\)
2: Chứng Minh với \(\forall N\in Z\) thì B= \(3^{n+2}-2^{n+2}+3^n-2^n⋮10\)
2:
\(B=3^{n+2}-2^{n+2}+3^n-2^n\)
\(=3^n\cdot9+3^n-2^n\cdot4-2^n\)
\(=3^n\cdot10-2^n\cdot5\)
\(=3^n\cdot10-2^{n-1}\cdot10⋮10\)
Đúng 0
Bình luận (0)
Chứng minh các mệnh đề sau
\(a,\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{n\left(n+1\right)}=\dfrac{n}{n+1}\) \(\forall n\in N\) *
\(b,1+\dfrac{1}{2^2}+...+\dfrac{1}{n^2}< 2-\dfrac{1}{n}\forall n\ge2\)
a: \(VT=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{n+1-1}{n+1}=\dfrac{n}{n+1}\)
Đúng 0
Bình luận (0)
Chứng minh \(\forall\) n \(\in\) N, n > 1 ta có \(\dfrac{1}{n-1}-\dfrac{1}{n}>\dfrac{1}{n^2}>\dfrac{1}{n}-\dfrac{1}{n+1}\)
Chứng minh các mệnh đề sau:
\(a,1^2+2^2+...+n^2=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}\) \(\forall n\in N\) *
\(b,1.2+2.3+...+n\left(n+1\right)=\dfrac{n\left(n+1\right)\left(n+2\right)}{3}\) \(\forall n\in N\) *