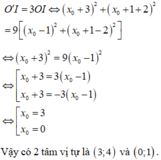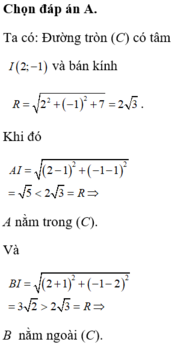trong mặt phẳng oxy cho đường tròn (C) x2 + y2 - 6x + 2y + 5 = 0
MD
Những câu hỏi liên quan
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C):
x
2
+
y
2
-
2
x
-
4
y
+
4
0
và đường tròn (C):
x
2
+
y
2
+
6
X
+
4
y
+
4
0...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C): x 2 + y 2 - 2 x - 4 y + 4 = 0 và đường tròn (C'): x 2 + y 2 + 6 X + 4 y + 4 = 0 Tìm tâm vị tự của hai đường tròn?
A. I(0;1) và J(3;4)
B. I(-1;-2) và J(3;2)
C. I(1;2) và J(-3;-2)
D. I(1;0) và J(4;3)
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C) :
x
2
+
y
2
-
2
x
-
4
y
+
4
0
và đường tròn (C) :
x
2
+
y
2
+
6
x
+
4
y
+
4
0
Tìm tâm vị trí của hai đường tròn? A. I(0;1) và J(3;4) B. I(-1;-2) và J(3;2) C. I(1;2) và J(-3;-2) D. I(1;0...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C) : x 2 + y 2 - 2 x - 4 y + 4 = 0 và đường tròn (C') : x 2 + y 2 + 6 x + 4 y + 4 = 0 Tìm tâm vị trí của hai đường tròn?
A. I(0;1) và J(3;4)
B. I(-1;-2) và J(3;2)
C. I(1;2) và J(-3;-2)
D. I(1;0) và J(4;3)
Trong mặt phẳng tọa độ Oxy, cho hai đường tròn
C
:
x
2
+
y
2
+
2
m
-
2
y
-
6
x
+
12
+
m
2
0
và
C
:
x...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hai đường tròn C ' : x 2 + y 2 + 2 m - 2 y - 6 x + 12 + m 2 = 0 và C : x + m 2 + y - 2 2 = 5 . Vectơ v → nào dưới đây là vectơ của phép tịnh tiến biến (C) thành (C')
A. v → = 2 ; 1
B. v → = - 2 ; 1
C. v → = - 1 ; 2
D. v → = 2 ; - 1
Đáp án A
Xét C ' : x - 3 2 + y + m - 2 2 = 1 - 4 m có tâm I'(3;2 - m) bán kính R ' = 1 - 4 m
Và đường tròn C : x + m 2 + y - 2 2 = 5 có tâm I(-m;2) bán kính R = 5
Vì (C’) là ảnh của (C ) qua T v → ⇒ R = R ' T v → ( I ) = I ' ⇔ 1 - 4 m = 5 I I ' → = I ' ⇔ m = - 1 v → = 3 + m ; - m ⇒ v → = ( 2 ; 1 ) .
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho hai đường tròn
C
:
x
2
+
y
2
+
2
m
-
2
y
-
6
x
+
12
+
m
2
0
và
C
...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hai đường tròn C ' : x 2 + y 2 + 2 m - 2 y - 6 x + 12 + m 2 = 0 và C x + m 2 + y - 2 2 = 5 Vecto v → nào dưới đây là vecto của phép tính tịnh tiến biến (C) thành (C')
A. v → = 2 ; 1
B. v → = - 2 ; 1
C. v → = - 1 ; 2
D. v → = 2 ; - 1
Trong mặt phẳng với hệ tọa độ
Ox
y
cho đường tròn
C
:
x
2
+
y
2
−
2
x
−
4
y
+
4
0
và đường tròn
C
:
x
2
+
y
2
+
6
x...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Ox y cho đường tròn C : x 2 + y 2 − 2 x − 4 y + 4 = 0 và đường tròn C ' : x 2 + y 2 + 6 x + 4 y + 4 = 0. Tìm tâm vị tự của hai đường tròn?
A. I 0 ; 1 v à J 3 ; 4
B. I − 1 ; − 2 v à J 3 ; 2
C. I 1 ; 2 v à J − 3 ; − 2
D. I 1 ; 0 v à J 4 ; 3
Đáp án A
Đường tròn C có tâm K 1 ; 2 , bán kính R = 1 + 4 − 4 = 1 .
Đường tròn C ' có tâm K ' − 3 ; − 2 , bán kính R ' = 9 + 4 − 4 = 3.
Giả sử V 1 ; k C = C '
khi đó k = R ' R ⇒ k = 3 ⇔ k = ± 3
Với k = 3 ⇒ I K ' → = 3 I K → ⇒ − 3 − x 1 = 3 1 − x 1 − 2 − y 1 = 3 2 − y 1 ⇒ I 3 ; 4
Với k = − 3 ⇒ I K ' → = − 3 I K → ⇒ − 3 − x 1 = − 3 1 − x 1 − 2 − y 1 = − 3 2 − y 1 ⇒ I 0 ; 1
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x2 + y2 - 2x + 6x - 6 =0.Tiếp tuyến của (C) vuông góc với đường thẳng: 6x+8y-3=0 , có phương trình là ax+by+c=0 (a<5, c<0). Tính 2a+5b-c=?
Đường tròn (C) tâm I(1;-3) bán kính \(R=4\)
Tiếp tuyến d vuông góc với 6x+8y-3=0 nên nhận \(\left(4;-3\right)\) là 1 vtpt
Tiếp tuyến d có dạng: \(4x-3y+c=0\)
\(d\left(I;d\right)=R\Leftrightarrow\dfrac{\left|4.1-3.\left(-3\right)+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=4\)
\(\Leftrightarrow\left|c+13\right|=20\Rightarrow\left[{}\begin{matrix}c=7\left(loại\right)\\c=-33\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=4\\b=-3\\c=-33\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C) : x2 + y2 – 2x + 2y + 1 0Phương trình đường tròn (C’) đối xứng (C) qua trục tung là: A.
(
x
−
1
)
2
+
(
y
−
1
)
2
1
B.
(
x...
Đọc tiếp
Trong mặt phẳng với hệ toạ độ Oxy, cho đường tròn (C) : x2 + y2 – 2x + 2y + 1 = 0
Phương trình đường tròn (C’) đối xứng (C) qua trục tung là:
A. ( x − 1 ) 2 + ( y − 1 ) 2 = 1
B. ( x + 1 ) 2 + ( y − 1 ) 2 = 2
C. ( x + 1 ) 2 + ( y + 1 ) 2 = 2
D. ( x + 1 ) 2 + ( x + 1 ) 2 = 1
Đáp án D
(C) có tâm I( 1; – 1), bán kính 1
Đ O y : I => I’( – 1; – 1 )
Phương trình đường tròn (C’): ( x + 1 ) 2 + ( y + 1 ) 2 = 1
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường tròn
(
C
)
:
x
2
+
y
2
-
4
x
+
2
y
-
7
0
và hai điểm A(1;1) và B(-1;2). Khẳng định nào dưới đây là đúng? A. A nằm trong và B nằm ngoài (C). B. A và B cùng nằm ngoài (C). C. A nằm ngoài và B nằm trong (C). D. A và B cùng nằm trong (C)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn ( C ) : x 2 + y 2 - 4 x + 2 y - 7 = 0 và hai điểm A(1;1) và B(-1;2). Khẳng định nào dưới đây là đúng?
A. A nằm trong và B nằm ngoài (C).
B. A và B cùng nằm ngoài (C).
C. A nằm ngoài và B nằm trong (C).
D. A và B cùng nằm trong (C)
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn
C
1
:
x
2
+
y
2
−
2
x
−
2
y
−
2
0
và
C
2
:
x
2
+
y
2
+
12...
Đọc tiếp
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn C 1 : x 2 + y 2 − 2 x − 2 y − 2 = 0 và C 2 : x 2 + y 2 + 12 x − 16 y = 0. Phép đồng dạng F tỉ số k biến C 1 thành C 2 Tìm k ?
A. k = 1 5
B. k= -6
C. k= 2
D. k= 5
Đáp án D
Ta có:
C 1 : x − 1 2 + y − 1 2 = 4 ⇒ R 1 = 2 ; C 2 : x + 6 2 + y − 8 2 = 100 ⇒ R 2 = 10
⇒ k = R 2 R 1 = 10 2 = 5.
Đúng 0
Bình luận (0)