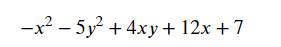
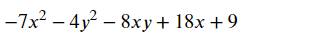 Tìm GTLN của biểu thức sau
Tìm GTLN của biểu thức sau
Tìm GTLN của các biểu thức sau:
a)3-x^2+2x (GTLN)
b)4X^2-20X+40(GTLN)
TL
Giá trị của biểu thức lớn nhất khi mẫu số nhỏ nhất.
Ta có x2 + 4x + 2013 = x2 + 4x + 4 + 2009 = (x + 2)2 + 2009 >= 2009.
Biểu thức trên nhỏ nhất sẽ = 2009 khi (x + 2)2 = 0. Suy ra x = -2.
Vậy GTLN = 2012/2009.
Tìm GTLN của Biểu thức sau
-x2-y2+xy+2x+2y
\(-x^2-y^2+xy+2x+2y=-\left[x^2-x\left(y+2\right)+\dfrac{1}{4}\left(y+2\right)^2\right]-\left(\dfrac{3}{4}y^2-3y+3\right)+4=-\left(x-\dfrac{1}{2}y-1\right)^2-\left(\dfrac{\sqrt{3}}{2}y-\sqrt{3}\right)^2+4\le4\)
\(max=4\Leftrightarrow\)\(\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)
Tìm GTNN của biểu thức sau:
1)A=\(\dfrac{b^2}{b-1}\), b>1
Tìm GTLN của biểu thức sau:
1)B=\(\dfrac{\sqrt{b-2}}{b},b>2\)
\(A=\dfrac{b^2}{b-1}=\dfrac{b^2-1+1}{b-1}=b+1+\dfrac{1}{b-1}=b-1+\dfrac{1}{b-1}+2\)
Áp dụng BĐT cosi cho \(b>0\left(b>1\right)\)
\(A=b-1+\dfrac{1}{b-1}+2\ge2\sqrt{\left(b-1\right)\cdot\dfrac{1}{b-1}}+2=2+2=4\)
Dấu \("="\Leftrightarrow\left(b-1\right)^2=1\Leftrightarrow\left[{}\begin{matrix}b-1=1\\b-1=-1\left(ktm\right)\end{matrix}\right.\Leftrightarrow b=2\left(tm\right)\)
Tìm GTLN, GTNN của biểu thức sau: P=5/căn(x) - 2
\(\sqrt{x}-2>=-2\)
=>\(P=\dfrac{5}{\sqrt{x}-2}< =-\dfrac{5}{2}\)
Dấu = xảy ra khi x=0
Vậy: Giá trị lớn nhất của P là -5/2 khi x=0
Tìm GTLN của biểu thức sau :
A = -x² - y² + xy + 2y + 2x
Tìm GTLN của biểu thức sau
P= 2017- /2x-3/
\(\left|2x-3\right|\ge0\)
\(\Rightarrow2017-\left|x-3\right|\le2017\)
Vậy giá trị lớn nhất của P là 2017 khi |2x - 3| = 0 <=> x = 3/2
Ta có: \(\left|2x-3\right|\) lớn hơn hoặc bằng 0
=> \(P=2017-\left|2x-3\right|\) < hơn hoặc = 2017
Dấu '=' xảu ra khi: \(2x-3=0\)
=> \(2x=-3\)
=> \(x=-\frac{3}{2}\)
Tìm GTLN và GTNN của biểu thức sau : (x+1)/(x^2+ x+1)
Đặt T là biểu thức cần tìm
Ta có:
\(\Leftrightarrow Tx^2+Tx+T-x-1=0\)
\(\Leftrightarrow Tx^2+x\left(T-1\right)+T-1=0\)
TH1: T = 1 => x= 0
TH2: \(T\ne0\)
delta \(\ge0\Leftrightarrow\left(T-1\right)^2-4.T.\left(T-1\right)\ge0\)
\(\Leftrightarrow T^2-2T+1-4T^2+4T\Leftrightarrow-3T^2+2T+1\ge0\Leftrightarrow-\dfrac{1}{3}\le T\le1\)
\(T_{min}=-\dfrac{1}{3}\Rightarrow\) thế vào ra x
\(T_{max}=1\Rightarrow\) thế vào ra x
*) Tìm Max \(P=\dfrac{x+1}{x^2+x+1}=\dfrac{x^2+x+1-x^2}{x^2+x+1}=1-\dfrac{x^2}{x^2+x+1}\le1\)
"=" xảy ra <=> x = 0
Tìm GTLN và GTNN của biểu thức sau : 4x+1/ x^2+2x+2
là \(4x+\dfrac{1}{x^2}+2x+2\) hay là \(\dfrac{4x+1}{x^2+2x+2}\) cái neog:0
\(P=\dfrac{4x+1}{x^2+2x+2}=\dfrac{x^2+2x+2-x^2+2x-1}{x^2+2x+2}=1-\dfrac{\left(x-1\right)^2}{x^2+2x+2}\le1\)
"=" xảy ra <=> x - 1 = 0 <=> x = 1
Vậy Max P = 1 <=> x = 1
P = \(\dfrac{4x+1}{x^2+2x+2}=\dfrac{-4x^2-8x-8+4x^2+12x+9}{x^2+2x+2}=-4+\dfrac{\left(2x+3\right)^2}{x^2+2x+2}\)
\(\ge-4\)
"=" xảy ra <=> 2x + 3 = 0 <=> x = -1,5
Vậy Min P = -4 <=> x = -1,5