\(ĐKXĐ:\left\{{}\begin{matrix}\dfrac{x^2}{x+1}\ge0\\x+1\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+1\ge0\\x\ne-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x\ne-1\end{matrix}\right.\Leftrightarrow x>-1\)

ĐKXĐ: \(-\dfrac{2}{x-1}>=0\)

=>x-1<0

=>x<1

1) ĐKXĐ: \(x\notin\left\{0;1\right\}\)

2) Ta có: \(A=\left(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right):\left(1-\dfrac{3-\sqrt{x}}{\sqrt{x}+1}\right)\)

\(=\dfrac{x+\sqrt{x}+1-\left(x-\sqrt{x}+1\right)}{\sqrt{x}}:\dfrac{\sqrt{x}+1-3+\sqrt{x}}{\sqrt{x}+1}\)

\(=2\cdot\dfrac{\sqrt{x}+1}{2\sqrt{x}-2}\)

\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)

a: ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)

Ta có: \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}+1}+\dfrac{2}{x-1}\right)\)

\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(=\dfrac{x-1}{\sqrt{x}}\)

b: Thay \(x=3+2\sqrt{2}\) vào P, ta được:

\(P=\dfrac{2\sqrt{2}+2}{\sqrt{2}+1}=2\)

a) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)

b) Thay x=0 vào A, ta được:

\(A=\dfrac{15\cdot\sqrt{0}-11}{0+2\sqrt{0}-3}-\dfrac{3\sqrt{0}-2}{\sqrt{0}-1}-\dfrac{2\sqrt{0}+3}{\sqrt{0}+3}\)

\(=\dfrac{-11}{-3}-\dfrac{-2}{-1}-\dfrac{3}{3}\)

\(=\dfrac{11}{3}-2-1\)

\(=\dfrac{11}{3}-\dfrac{9}{3}=\dfrac{2}{3}\)

\(a,ĐK:x>0;x\ne1\\ b,A=\dfrac{1+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}+1}=\dfrac{\sqrt{x}-1}{\sqrt{x}}\\ c,x=4\Leftrightarrow\sqrt{x}=2\Leftrightarrow A=\dfrac{2-1}{2}=\dfrac{1}{2}\)

a) ĐKXĐ: \(x>0;x\ne4\)

\(Q=\left(\dfrac{\sqrt{x}-1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\right):\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{x}+1}\right)\)

\(=\left[\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\right]:\dfrac{\sqrt{x}+1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\)

\(=\dfrac{x-1-\left(x-4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}:\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)

\(=\dfrac{3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\cdot\sqrt{x}\left(\sqrt{x}+1\right)\)

\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)

b) Để biểu thức \(Q\) có giá trị âm thì \(\dfrac{3\sqrt{x}}{\sqrt{x}-2}< 0\)

\(\Rightarrow\sqrt{x}-2< 0\) (vì \(3\sqrt{x}>0\forall x>0;x\ne4\))

\(\Leftrightarrow\sqrt{x}< 2\Leftrightarrow0\le x< 4\) 

Kết hợp với điều kiện xác định của \(x\), ta được: \(0< x< 4\)

\(\text{#}\mathit{Toru}\)

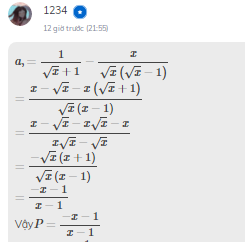
Mk ra đáp án khác với đáp án ủa bn nên bn bào sai chứ j, thật ra cả 2 đáp án đều giống nhau, do biến đổi dấu nên trở thành 2 đáp án khác nhau thôi :V

để mk lm lại phần đáp án của mk ra giống đáp án của bn nek :V

\(a,\)\(P=\dfrac{-x-1}{x-1}\)

\(\Rightarrow\dfrac{-\left(-x-1\right)}{-\left(x-1\right)}=\dfrac{x-1}{-x+1}=\dfrac{x-1}{1-x}\)

Còn câu b thì hôm qua bn ghi là \(x=\dfrac{1}{\sqrt{2}}\) chứ có pk là \(1\sqrt{2}\) đou >:V

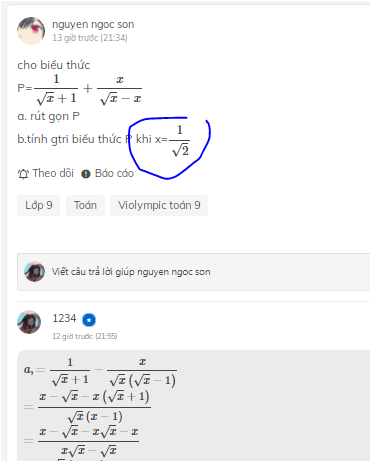
\(b,\)Thay \(x=1\sqrt{2}\) vào \(P\) ta có :

\(P=\dfrac{x-1}{1-x}\)

\(P=\dfrac{1\sqrt{2}-1}{1-1\sqrt{2}}=3+2\sqrt{2}\)