Question

cho biểu thức 

P=\(\dfrac{1}{\sqrt{x}+1}+\dfrac{\sqrt{x}+1}{\sqrt{x}}\)

a. rút gọn P

b.tính gtri biểu thức P khi x=1√2

đáp án:

a.P=\(\dfrac{x+1}{1-x}\)

b.P=3+2\(\sqrt{2}\)

mk chỉ bt đáp án chứ ko bt cách giải

Answer 1

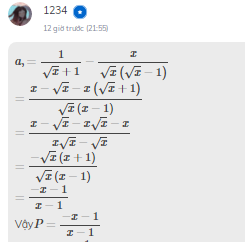
Mk ra đáp án khác với đáp án ủa bn nên bn bào sai chứ j, thật ra cả 2 đáp án đều giống nhau, do biến đổi dấu nên trở thành 2 đáp án khác nhau thôi :V

để mk lm lại phần đáp án của mk ra giống đáp án của bn nek :V

\(a,\)\(P=\dfrac{-x-1}{x-1}\)

\(\Rightarrow\dfrac{-\left(-x-1\right)}{-\left(x-1\right)}=\dfrac{x-1}{-x+1}=\dfrac{x-1}{1-x}\)

Còn câu b thì hôm qua bn ghi là \(x=\dfrac{1}{\sqrt{2}}\) chứ có pk là \(1\sqrt{2}\) đou >:V

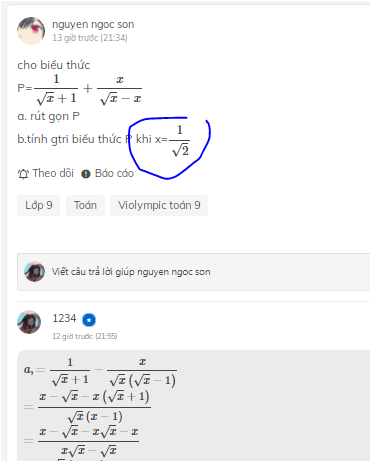
\(b,\)Thay \(x=1\sqrt{2}\) vào \(P\) ta có :

\(P=\dfrac{x-1}{1-x}\)

\(P=\dfrac{1\sqrt{2}-1}{1-1\sqrt{2}}=3+2\sqrt{2}\)