Nhờ mn giúp em vs ạ.
TN
Những câu hỏi liên quan
Nhờ mn giúp em vs ạ.
Nhờ mn giúp em vs ạ. Em cảm ơn nhìu
a: Xét (O) có
ΔABN nội tiếp
AB là đường kính
Do đó: ΔABN vuông tại N
=>AN\(\perp\)NB tại N
=>BN\(\perp\)AM tại N
Xét (O) có
ΔAHB nội tiếp
AB là đường kính
Do đó: ΔAHB vuông tại H
=>AH\(\perp\)HB tại H
=>BH\(\perp\)AD tại H
Xét ΔBAM vuông tại B có BN là đường cao
nên \(AN\cdot AM=AB^2\left(1\right)\)
Xét ΔABD vuông tại B có BH là đường cao
nên \(AH\cdot AD=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AN\cdot AM=AH\cdot AD\)
c: ta có: ΔOAN cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)AN
Xét ΔIAO vuông tại I và ΔNBM vuông tại N có
\(\widehat{IAO}=\widehat{NBM}\left(=90^0-\widehat{AMB}\right)\)
Do đó: ΔIAO~ΔNBM
Xét tứ giác OIMB có
\(\widehat{OBM}+\widehat{OIM}=90^0+90^0=180^0\)
nên OIMB là tứ giác nội tiếp
=>\(\widehat{MOB}=\widehat{MIB}\)
Xét ΔOBM vuông tại B và ΔINB vuông tại N có
\(\widehat{BOM}=\widehat{NIB}\left(cmt\right)\)
Do đó: ΔOBM~ΔINB
Đúng 1
Bình luận (0)
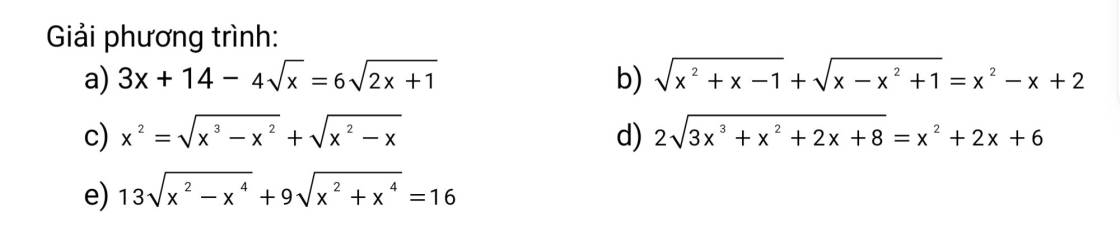 Nhờ mn giúp em vs ạ. c.ơn nhìu
Nhờ mn giúp em vs ạ. c.ơn nhìu
a: \(3x-12-4\sqrt{x}+8=6\sqrt{2x+1}-18\)
=>\(\left(x-4\right)\cdot3-4\left(\sqrt{x}-2\right)=6\left(\sqrt{2x+1}-3\right)\)
=>\(3\left(x-4\right)-\dfrac{4\left(x-4\right)}{\sqrt{x}+2}-6\cdot\dfrac{2x+1-9}{\sqrt{2x+1}+3}=0\)
=>\(\left(x-4\right)\left(3-\dfrac{4}{\sqrt{x}+2}-\dfrac{12}{\sqrt{2x+1}+3}\right)=0\)
=>x-4=0
=>x=4
b: \(\Leftrightarrow\sqrt{x^2+x-1}-1+\sqrt{x-x^2+1}-1=x^2-x\)
=>\(\dfrac{x^2+x-1-1}{\sqrt{x^2+x-1}+1}+\dfrac{x-x^2+1-1}{\sqrt{x-x^2+1}+1}=x\left(x-1\right)\)
=>\(\dfrac{\left(x+2\right)\left(x-1\right)}{\sqrt{x^2+x-1}+1}-\dfrac{x\left(x-1\right)}{\sqrt{x-x^2+1}+1}-x\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(\dfrac{x+2}{\sqrt{x^2+x-1}+1}-\dfrac{x}{\sqrt{x-x^2+1}+1}-x\right)=0\)
=>x-1=0
=>x=1
c: \(\Leftrightarrow x^2-\sqrt{x^3-x^2}-\sqrt{x^2-x}=0\)
=>\(\sqrt{x}\left(x\sqrt{x}-\sqrt{x^2-x}-\sqrt{x-1}\right)=0\)
=>căn x=0
=>x=0
Đúng 0
Bình luận (0)
Nhờ mn giúp em vs ạ. Cảm ơn nhìu.
Bài 3:
b: Gọi K là giao điểm của AB và OP
Xét (O) có
PA,PB là các tiếp tuyến
Do đó: PA=PB
=>P nằm trên đường trung trực của BA(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra PO là đường trung trực của AB
=>PO\(\perp\)AB tại K và K là trung điểm của AB
Ta có: ΔOAP vuông tại A
=>\(AP^2+AO^2=OP^2\)
=>\(AP^2=OP^2-OA^2=d^2-R^2\)
=>\(AP=\sqrt{d^2-R^2}\)
Xét ΔOAP vuông tại A có AK là đường cao
nên \(AK\cdot OP=AO\cdot AP\)
=>\(AK\cdot d=R\cdot\sqrt{d^2-R^2}\)
=>\(AK=\dfrac{R\cdot\sqrt{d^2-R^2}}{d}\)
K là trung điểm của AB
=>\(AB=2\cdot AK=\dfrac{2\cdot R\cdot\sqrt{d^2-R^2}}{d}\)
Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>\(BA^2+AC^2=BC^2\)
=>\(AC^2=\left(2R\right)^2-\left(\dfrac{2R\sqrt{d^2-R^2}}{d}\right)^2\)
=>\(AC^2=4R^2-\dfrac{4R^2\cdot\left(d^2-R^2\right)}{d^2}\)
=>\(AC^2=\dfrac{4R^2d^2-4R^2\left(d^2-R^2\right)}{d^2}=\dfrac{4R^4}{d^2}\)
=>\(AC=\dfrac{2R^2}{d}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AC\cdot AB\)
=>\(AH\cdot2R=\dfrac{2R^2}{d}\cdot\dfrac{2R\sqrt{d^2-R^2}}{d}\)
=>\(AH=\dfrac{R\cdot2R\sqrt{d^2-R^2}}{d^2}=\dfrac{2R^2\cdot\sqrt{d^2-R^2}}{d^2}\)
Đúng 2
Bình luận (0)
Ác nào giúp em ạ đc bài nào hay bài ấy ạ nhờ mn githich dễ hiểu cho e vs ak
Bạn cần giải thích bài nào nhỉ?
Đúng 0
Bình luận (0)
Dạ nhờ Mn chỉ em câu 1 vs 5 2 câu đấy em không biết cách xác định thì của nó ạ, dạ cũng mong mn xem cậu 2, 3,4 của em làm nó có sai chỗ nào không ạ, dạ nếu có sai mong mn chỉ ra giúp em ạ
Dạ em cảm ơn MN TRƯỚC ạ 

Nhờ mn giúp mik vs ạ
\(n_{Fe}=a;n_{Cu}=b\\ 56a+64b=9,2\left(I\right)\\ BTe^{^{ }-}:3a+2b=2n_{SO_2}\left(II\right)\\ n_{H_2SO_4pư}=n_{SO_2}+1,5a+b\\ n_{H_2SO_4sau}=\dfrac{50.0,98}{98}-n_{SO_2}-1,5a-b=0,5-n_{SO_2}-1,5a-b\\ m_{ddsau}=9,2+50-64n_{SO_2}=59,2-64n_{SO_2}\\ \Rightarrow:\dfrac{98\left(0,5-n_{SO_2}-1,5a-b\right)}{59,2-64n_{SO_2}}=\dfrac{30,625}{100}\left(III\right)\\ \Rightarrow a=0,05;b=0,1;n_{SO_2}=0,175mol\\ V=0,175.22,4=3,92L\\ \%m_{Fe}=\dfrac{0,05.56}{9,2}.100\%=30,43\%\\ \%m_{Cu}=69,57\%\)
Đúng 3
Bình luận (0)
 Nhờ mn giúp mik vs ạ
Nhờ mn giúp mik vs ạ
Nhờ mn giúp mik vs ạ.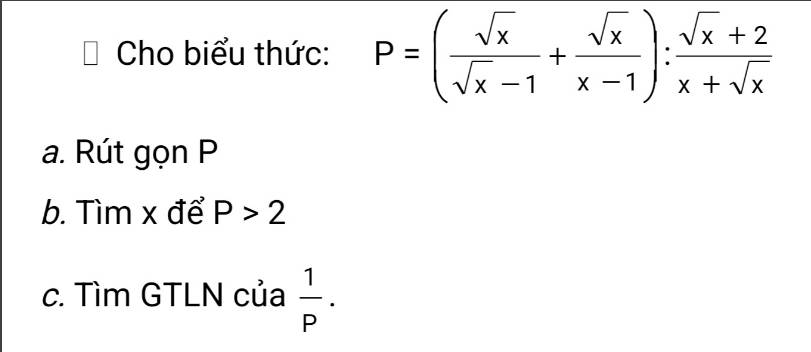
Lời giải:
a. ĐKXĐ: $x>0; x\neq 1$
\(P=\left[\frac{\sqrt{x}(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}+\frac{\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}\right].\frac{x+\sqrt{x}}{\sqrt{x}+2}\)
\(=\frac{x+\sqrt{x}+\sqrt{x}}{(\sqrt{x}-1)(\sqrt{x}+1)}.\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+2}=\frac{\sqrt{x}(\sqrt{x}+2)}{(\sqrt{x}-1)(\sqrt{x}+1)}.\frac{\sqrt{x}(\sqrt{x}+1)}{\sqrt{x}+2}=\frac{x}{\sqrt{x}-1}\)
b.
$P>2 \Leftrightarrow \frac{x}{\sqrt{x}-1}-2>0$
$\Leftrightarrow \frac{x-2\sqrt{x}+2}{\sqrt{x}-1}>0$
$\Leftrightarrow \frac{(\sqrt{x}-1)^2+1}{\sqrt{x}-1}>0$
$\Leftrightarrow \sqrt{x}-1>0$ (do $(\sqrt{x}-1)^2+1>0$)
$\Leftrightarrow x>1$
Kết hợp đkxđ suy ra $x>1$
c.
$\frac{1}{P}=\frac{\sqrt{x}-1}{x}$
Áp dụng BĐT Cô-si:
$x+4\geq 4\sqrt{x}\Rightarrow x\geq 4(\sqrt{x}-1)$
$\Rightarrow \frac{\sqrt{x}-1}{x}\leq \frac{\sqrt{x}-1}{4(\sqrt{x}-1)}=\frac{1}{4}$
Vậy $\frac{1}{P}$ max $=\frac{1}{4}$ khi $x=4$
Đúng 2
Bình luận (1)




