a: Xét (O) có
ΔABN nội tiếp
AB là đường kính
Do đó: ΔABN vuông tại N
=>AN\(\perp\)NB tại N
=>BN\(\perp\)AM tại N
Xét (O) có
ΔAHB nội tiếp
AB là đường kính
Do đó: ΔAHB vuông tại H
=>AH\(\perp\)HB tại H
=>BH\(\perp\)AD tại H
Xét ΔBAM vuông tại B có BN là đường cao
nên \(AN\cdot AM=AB^2\left(1\right)\)
Xét ΔABD vuông tại B có BH là đường cao
nên \(AH\cdot AD=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AN\cdot AM=AH\cdot AD\)
c: ta có: ΔOAN cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)AN
Xét ΔIAO vuông tại I và ΔNBM vuông tại N có
\(\widehat{IAO}=\widehat{NBM}\left(=90^0-\widehat{AMB}\right)\)
Do đó: ΔIAO~ΔNBM
Xét tứ giác OIMB có
\(\widehat{OBM}+\widehat{OIM}=90^0+90^0=180^0\)
nên OIMB là tứ giác nội tiếp
=>\(\widehat{MOB}=\widehat{MIB}\)
Xét ΔOBM vuông tại B và ΔINB vuông tại N có
\(\widehat{BOM}=\widehat{NIB}\left(cmt\right)\)
Do đó: ΔOBM~ΔINB




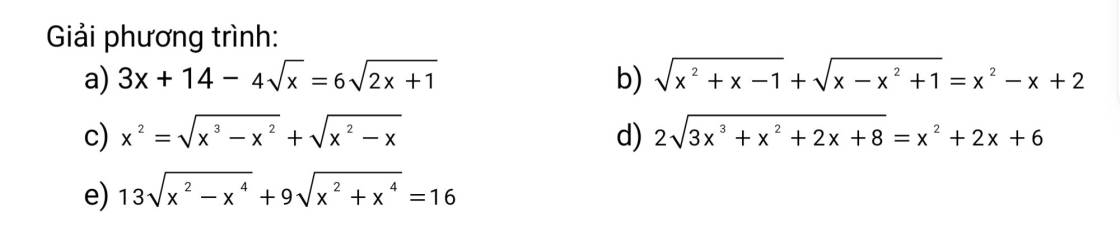 Nhờ mn giúp em vs ạ. c.ơn nhìu
Nhờ mn giúp em vs ạ. c.ơn nhìu







