Cho vuông tại là trung điểm của Kẻ tại E, kẻ tại F; H là điểm đối xứng với I qua F
a) Chứng minh tứ giác là hình chữ nhật
b) Chứng minh tứ giác là hình bình hành
c) Chứng minh tứ giác AICH là hình thoi
cho tam gvác abc vuông tại a trung tuyến am, đường cao ah .kẻ hd vuông góc với ab tại d ,he vuông góc ac tại e .a,chứng minh ah=de b,kẻ mf vuông góc vớv ab tại f lấy điểm k sao cho f là trung điểm của mk chứng minh tứ giác ambk la hinhf thoi và am vuông góc với de c, chứng minh bd.ac+ce.ab=ab.ac
Cho tam giác ABC có AB = AC, D là trung điểm của BC. c.) Kẻ DE vuông góc với AB tại E, kẻ DF vuông góc với MC tại F. Chứng minh E, D, F thẳng hàng. Giúp mình đi mn
Cho tam giác ABC vuông tại A có đường trung tuyến AM. Kẻ ME vuông góc AB tại E, MF vuông góc AC tại F.
a) Tứ giác AEMF là hình gì? Vì sao?
b) Chứng minh F là trung điểm của AC
a: Xét tứ giác AEMF có
\(\widehat{AEM}=\widehat{AFM}=\widehat{FAE}=90^0\)
=>AEMF là hình chữ nhật
b: ta có: MF\(\perp\)AC
AB\(\perp\)AC
Do đó: MF//AB
Xét ΔABC có
M là trung điểm của BC
MF//AB
Do đó: F là trung điểm của AC
Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC ở D. Kẻ DE vuông góc với AC tại E.
a, CM: DA=DE.
b, CM: BD là trung trực của AE.
c, Kẻ CK vuông góc với BD tại K, đường thẳng CK; DA cắt nhau tại F. CM: 3 điểm D; E; F thẳng hàng.
Bạn nào biết làm giúp mình với !!!(kiêm luôn vẽ hình)
Cho tam giác ABC vuông tại A , có AB=4cm AC = 6cm kẻ đường cao AH từ H kẻ HE vuông góc với AB tại E từ H kẻ HK vuông góc với AC tại F. Gọi I và K lần lượt là trung điểm của HB và HC lấy điểm M trên đoạn FC sao cho FA=FM
Cho tam giác ABC vuông tại A có đường trung tuyến AM. Kẻ ME vuông góc AB tại E, MF vuông góc AC
tại F.
a) Tứ giác AEMF là hình gì? Vì sao?
b) Chứng minh F là trung điểm của AC
c)
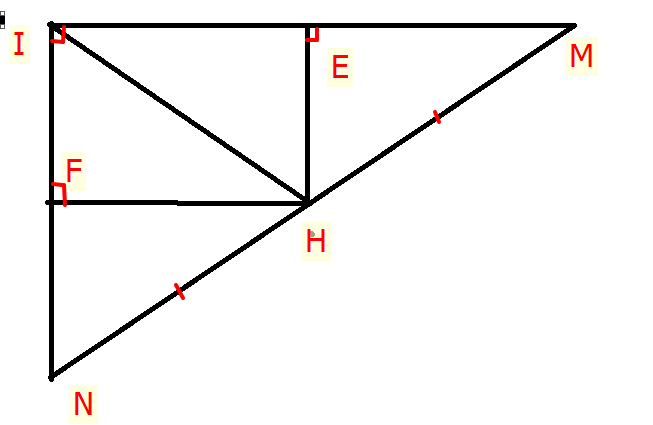
Cho IMN vuông tại I, H là trung điểm của MN. Biết MN = 12 (cm)
Từ H kẻ HE vuông góc IM tại E (E e IM) và HF vuông góc IN tại F (F e IN)
a)Tính IH.
b) Chứng minh IEHF là hình gi ? vì sao ?
a) Xét ΔNIM vuông tại I có : IH là đường trung tuyến
→ IH = \(\dfrac{1}{2}MN=\dfrac{1}{2}.12=6\)cm
b) Xét tứ giác IEFH có : \(\widehat{EIF}=\widehat{IFH\:}=\widehat{IEH}=90\)
→ IEHF là hình chữ nhật ( DHNB hình chữ nhật )
Cho ΔABC vuông cân tại A. Gọi D là trung điểm của BC. Trên đoạn AD lấy điểm E bất kì ( E≠AvàD). Qua E kẻ các đường vuông góc với AB,AC lần lượt tại M,N
a, Cm AMEN là hình vuông
b, Cm MN//BC
c, Qua M kẻ đường thẳng vuông góc với DN tại F. Cm góc AFE=90o
d, Cm B,E,F thẳng hàng
a: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là phân giác của \(\widehat{BAC}\)
Xét tứ giác AMEN có \(\widehat{AME}=\widehat{ANE}=\widehat{MAN}=90^0\)
=>AMEN là hình chữ nhật
Xét hình chữ nhật AMEN có AE là phân giác của \(\widehat{MAN}\)
nên AMEN là hình vuông
b: AMEN là hình vuông
=>\(\widehat{AMN}=45^0\)
=>\(\widehat{AMN}=\widehat{ABC}\)
mà hai góc này ở vị trí đồng vị
nên MN//BC
c: AMEN là hình vuông
=>A,M,E,N cùng thuộc đường tròn tâm O, đường kính là AE và MN
=>O là trung điểm chung của AE và MN(2)
\(\widehat{MFN}=90^0\)
=>F nằm trên đường tròn đường kính MN
=>F nằm trên (O)
Xét (O) có
ΔAFE nội tiếp
AE là đường kính
Do đó: ΔAFE vuông tại F
=>\(\widehat{AFE}=90^0\)
Cho tam giác ABC vuông tại A ( AB<AC) có Ae là đường trung tuyến. Từ E kẻ EF vuông góc AB tại Fvà kẻ EN Vuông góc AC tại N.
a) Chứng minh ANEF là hình chữ nhật
b) D là điểm đối xứng với E qua F. Chứng minh AEBD là hình thoi
c) K là giao điểm của AE và CF. Chứng minh AK= 2KE
d) I là trung điểm EF. Chứng minh bốn điểm B,I,K,N thẳng hàng
Mn giúp e với ạ, mai e phải nộp rồi :(
Xl bạn trình độ mik chỉ làm đc vậy thôi nha!
Chứng minh
a, Xét tứ giác ANEF có:
Góc NAF= 900 ( vì ΔABC vuông tại A)
Góc ANF= 900 (vì EN⊥ AC)
Góc AFE= 900 ( vì EF ⊥ AB)
⇒ Tứ giác ANEF là hình chữ nhật( đpcm)
b)Xét tam giác BAC vuông tại A có:
AE là đường trung tuyến(BE=EC)
\(\Rightarrow\)AE=BE=EC
Xét t/g AEBD có:
BF=FA(EF vuông góc BA)
DF=FE(D đx với E qua F)
\(\Rightarrow\)T/g AEBD là hbh
Mà AE=BE(cmt)
\(\Rightarrow\)T/g AEBD là hthoi