Cho h/c ABCD có ΔABC đều. M là trung điểm CD, AG⊥(BCD) tại G, biết G ϵ BM.
cm: AB⊥CD
Cho h/c ABCD có ΔABC đều. M là trung điểm CD, AG⊥(BCD) tại G, biết G ϵ BM.
cm: AB⊥CD
Cho h/c ABCD có ΔABC đều. M là trung điểm CD, AG⊥(BCD) tại G, biết G ϵ BM.
cm: AB⊥CD
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.
a) Tìm giao điểm A’ của đường thẳng AG và mp(BCD).
b) Qua M kẻ đường thẳng Mx song song với AA’ và Mx cắt (BCD) tại M’.
c) Chứng minh GA = 3GA’
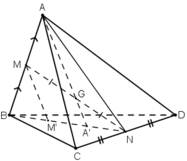
a) Có: MN ⊂ (ABN)
⇒ G ∈ (ABN)
⇒ AG ⊂ (ABN).
Trong (ABN), gọi A’ = AG ∩ BN.
⇒ A’ ∈ BN ⊂ (BCD)
⇒ A’ = AG ∩ (BCD).
b) + Mx // AA’ ⊂ (ABN) ; M ∈ (ABN)
⇒ Mx ⊂ (ABN).
M’ = Mx ∩ (BCD)
⇒ M’ nằm trên giao tuyến của (ABN) và (BCD) chính là đường thẳng BN.
⇒ B; M’; A’ thẳng hàng.
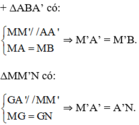
⇒ BM’ = M’A’ = A’N.
c) Áp dụng chứng minh câu b ta có:
ΔMM’N có: MM’ = 2.GA’
ΔBAA’ có: AA’ = 2.MM’
⇒ AA’ = 4.GA’
⇒ GA = 3.GA’.
Cho tứ diện ABCD ; gọi G là trọng tâm tam giác BCD và M là trung điểm CD; I là điểm ở trên đoạn thẳng AG; BI cắt (ACD) tại J. Chọn khẳng định sai?
A. giao tuyến của (ACD) và ( ABG) là AM
B. 3 điểm A; J; M thẳng hàng
C. J là trung điểm của AM
D. giao tuyến của (ACD) và ( BDJ) là DJ
Cho ΔABC , AB=AC , phân giác AD .
a, Chứng minh : ΔABD=ΔACD
b, Vẽ trung tuyến CF , G là giao điểm CF và AD . Chứng minh G là trọng tâm ΔABC
c, Gọi H là trung điểm của CD . Đường thẳng \(\perp\)CD tại H cắt AC tại E . Chứng minh : ΔDEC cân
d, So sánh AD và BD
a) Xét ΔABD và ΔACD có
AB=AC(ΔBAC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
b) Ta có: ΔABD=ΔACD(cmt)
nên BD=CD(hai cạnh tương ứng)
hay D là trung điểm của BC
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC(cmt)
CF là đường trung tuyến ứng với cạnh AB(gt)
AD cắt CF tại G(gt)
Do đó: G là trọng tâm của ΔABC(Tính chất ba đường trung tuyến của tam giác)
c) Ta có: ΔABD=ΔACD(cmt)
nên \(\widehat{ADB}=\widehat{ADC}\)(hai góc tương ứng)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
Xét ΔADC có
H là trung điểm của CD(gt)
HE//AD(cùng vuông góc với BC)
Do đó: E là trung điểm của AC(Định lí 1 về đường trung bình của tam giác)
Ta có: ΔADC vuông tại D(cmt)
mà DE là đường trung tuyến ứng với cạnh huyền AC(E là trung điểm của AC)
nên \(DE=\dfrac{AC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
hay DE=EC
Xét ΔDEC có ED=EC(cmt)
nên ΔDEC cân tại E(Định nghĩa tam giác cân)
Câu 31: Cho tứ diện đều ABCD. Gọi G là trọng tâm tam giác BCD. Góc giữa hai đường thẳng AG CD bằng bao nhiêu độ Câu 32: Cho tứ diện OABC có OA OB OC , đôi một vuông góc với nhau và OA= OB= OC Gọi M trung điểm AC.Góc giữa hai đường thẳng AB OM bằng ?° Câu 33: Trong không gian cho hai vectơ u v, có u v, 120 , u = 4, và v=3.Độ dài của vecto u-v bằng Câu 34: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh bên SA vuông góc với đáy, H,K lần lượt là hình chiếu của A lên SC, SD. Khẳng định nào sau đây đúng ? A. BC vuông góc SAC B. AK vuông góc SCD C. AH vuông góc SCD D. BD vuông góc SAC Câu 35: Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ và ? A. 900 B. 600 C. 450 D. 1200
Cau 33:
\(\left|\overrightarrow{u}-\overrightarrow{v}\right|=\sqrt{\left(\overrightarrow{u}-\overrightarrow{v}\right)^2}=\sqrt{u^2+v^2-2\cdot u\cdot v\cdot cos120}\)
\(=\sqrt{4^2+3^2-2\cdot4\cdot3\cdot\dfrac{-1}{2}}=\sqrt{37}\)
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác BCD và O là trung điểm AG
a) Chứng minh
30 OA OB OC OD + + + =
b) Biểu diễn
theo ba vecto , , . AG AB AC AD
c) Gọi M, N lần lượt là trung điểm AB, CD và I là trung điểm MN. Chứng minh ba
điểm A , I ,G thằng hàng và tim tỉ số AI/AG
cho hình thang cân ABCD (AB//CD) E, F, G , H lần lượt là trung điểm của AB, BC, CD, DA. Biết góc BCD = 60 độ. tính số đo các góc trong tứ giác EFGH
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN
a) Tìm giao điểm A' của đường thẳng AG và mặt phẳng (BCD)
b) Qua M kẻ đường thẳng Mx song song với AA' và Mx cắt (BCD) tại M'. Chứng minh B, M', A' thẳng hàng và BM'=M'A'=A'N
c) Chứng minh GA = 3 GA'
a) Trong (ABN): AG BN = A' => A'
BN, BN
(BCD) => A'
(BCD) => A' = AG
(BCD).
b) Chứng minh M' thuộc giao tuến A'B của (ABA') và (DBC)
c) Chứng minh GA' = MM' =
AA' => đpcm