Question

Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.

a) Tìm giao điểm A’ của đường thẳng AG và mp(BCD).

b) Qua M kẻ đường thẳng Mx song song với AA’ và Mx cắt (BCD) tại M’.

c) Chứng minh GA = 3GA’

Answer 1

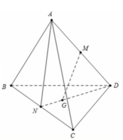
a) Có: MN ⊂ (ABN)

⇒ G ∈ (ABN)

⇒ AG ⊂ (ABN).

Trong (ABN), gọi A’ = AG ∩ BN.

⇒ A’ ∈ BN ⊂ (BCD)

⇒ A’ = AG ∩ (BCD).

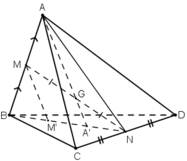
b) + Mx // AA’ ⊂ (ABN) ; M ∈ (ABN)

⇒ Mx ⊂ (ABN).

M’ = Mx ∩ (BCD)

⇒ M’ nằm trên giao tuyến của (ABN) và (BCD) chính là đường thẳng BN.

⇒ B; M’; A’ thẳng hàng.

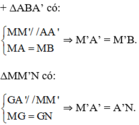
⇒ BM’ = M’A’ = A’N.

c) Áp dụng chứng minh câu b ta có:

ΔMM’N có: MM’ = 2.GA’

ΔBAA’ có: AA’ = 2.MM’

⇒ AA’ = 4.GA’

⇒ GA = 3.GA’.