Xác định m đẻ bất phương trình có nghiệm đúng với mọi x
(m2−4m+3)x+m−m2<0
Bài 3: xác định m để bất phương trình (m2-4m+3)x+m-m2<0 nghiệm đúng với mọi x
Xác định m đẻ bất phương trình có nghiệm đúng với mọi x
(m2−4m+3)x+m−m2<0
Xác định m đẻ bất phương trình có nghiệm đúng với mọi x
(m2−4m+3)x+m−m2<0
cần m^2 -4m +3 =0 => m=1 hoặc m=3
với m =1 => <0=> loiaj
với m=3 có -3 <0 đúng nhận
Xác định m đẻ bất phương trình có nghiệm đúng với mọi \(x\)
\(\left(m^2-4m+3\right)x+m-m^2< 0\)
Bài 3: Tìm m để bất phương trình: x2 - 2x + 1 - m2 ≤ 0 nghiệm đúng với ∀x ∈ [1; 2]. Bài 4: Tìm m để bất phương trình: (m - 1)x2 + (2 - m)x- 1 > 0 có nghiệm đúng với mọi∀x ∈ (1; 2). Bài 5: Tìm m để bất phương trình: 3(m - 2)x2 + 2(m + 1)x + m - 1 < 0 có nghiệm đúngvới mọi ∀x ∈ (-1; 3). Bài 6: Tìm m để bất phương trình m2 - 2mx + 4 > 0 có nghiệm đúng với mọi ∀x ∈ (-1;0,5)
3:
x^2-2x+1-m^2<=0
=>(x-1)^2-m^2<=0
=>(x-1)^2<=m^2
=>-m<=x-1<=m
=>-m+1<=x<=m+1
mà x thuộc [-1;2]
nên -m+1>=-1 và m+1<=2
=>-m>=-2 và m<=1
=>m<=2 và m<=1
=>m<=1
Bài 3: Tìm điều kiện để phương trình có nghiệm đúng với mọi x thuộc R
c)m²x = 9x+ m² - 4m +3
d)m2(x-1)-4mx=-5m+4
\(c,PT\Leftrightarrow m^2x-9x-\left(m^2-4m+3\right)=0\\ \Leftrightarrow x\left(m^2-9\right)-\left(m-3\right)\left(m-1\right)=0\)
PT có nghiệm đúng với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-9=0\\\left(m-3\right)\left(m-1\right)=0\end{matrix}\right.\Leftrightarrow m=3\)
\(d,PT\Leftrightarrow m^2x-m^2-4mx+5m-4=0\\ \Leftrightarrow x\left(m^2-4m\right)-\left(m^2-5m+4\right)=0\\ \Leftrightarrow xm\left(m-4\right)-\left(m-1\right)\left(m-4\right)=0\)
PT có nghiệm đúng với mọi x
\(\Leftrightarrow\left\{{}\begin{matrix}m\left(m-4\right)=0\\\left(m-4\right)\left(m-1\right)=0\end{matrix}\right.\Leftrightarrow m=4\)
Cho bất phương trình 3 + x + 6 - x - 18 + 3 x - x 2 ≤ m 2 - m + 1 (m là tham số). Có bao nhiêu giá trị nguyên của m thuộc[-5;5] để bất phương trình nghiệm đúng với mọi x ∈ - 3 ; 6 ?
A. 3
B. 5
C. 9
D. 10
Đặt ![]()
Suy ra ![]()
Ta có ![]()
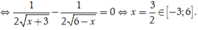
Ta có bảng biến thiên
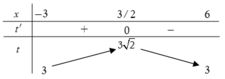
Từ bảng biến thiên ta suy ra ![]()
Khi đó bất phương trình trở thành: ![]()
![]()
Xét hàm số ![]() với
với ![]()
Ta có ![]()
Suy ra hàm số f(t) nghịch biến trên ![]()
![]()
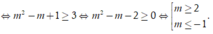
Chọn C.
Cho phương trình m 2 - 3 m + 2 x + m 2 + 4 m + 5 = 0 . Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm đúng với mọi x thuộc R.
A. m = −2.
B. m = −5.
C. m = 1.
D. Không tồn tại.
Phương trình đã cho nghiệm đúng với hay phương trình có vô số nghiệm khi
m 2 − 3 m + 2 = 0 − ( m 2 + 4 m + 5 ) = 0 ⇔ m = 1 m = 2 m ∈ ∅ ⇔ m ∈ ∅
Đáp án cần chọn là: D
Cho bất phương trình x2-6x +2(m+2)|x-3| +m2 +4m +12 >0
có bao nhiêu giá trị nguyên của m ϵ [-10;10] để bất phương tình đúng với mọi xϵ (-2;5)
\(\Leftrightarrow\left(x-3\right)^2+2\left(m+2\right)\left|x-3\right|+m^2+4m+3>0\)
Đặt \(\left|x-3\right|=t\Rightarrow0\le t< 5\)
\(\Rightarrow t^2+2\left(m+2\right)t+m^2+4m+3>0\) ;\(\forall t\in[0;5)\)
\(\Leftrightarrow\left(t+m+1\right)\left(t+m+3\right)>0\)
\(\Rightarrow-m-3< t< -m-1\)
Pt nghiệm đúng với mọi \(t\in[0;5)\) khi và chỉ khi
\(\left\{{}\begin{matrix}0>-m-3\\5\le-m-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>-3\\m\le-5\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn