 giúp e câu 1,2,3,4,5,12,13,14 vs ạ 🥲 e k hiểu lắm ạ
giúp e câu 1,2,3,4,5,12,13,14 vs ạ 🥲 e k hiểu lắm ạ
H24
Những câu hỏi liên quan
 giúp e câu 9,10 với ạ với coi giúp e mấy câu kia có sai k ạ tại e thấy cũng lạ lạ 🥲
giúp e câu 9,10 với ạ với coi giúp e mấy câu kia có sai k ạ tại e thấy cũng lạ lạ 🥲
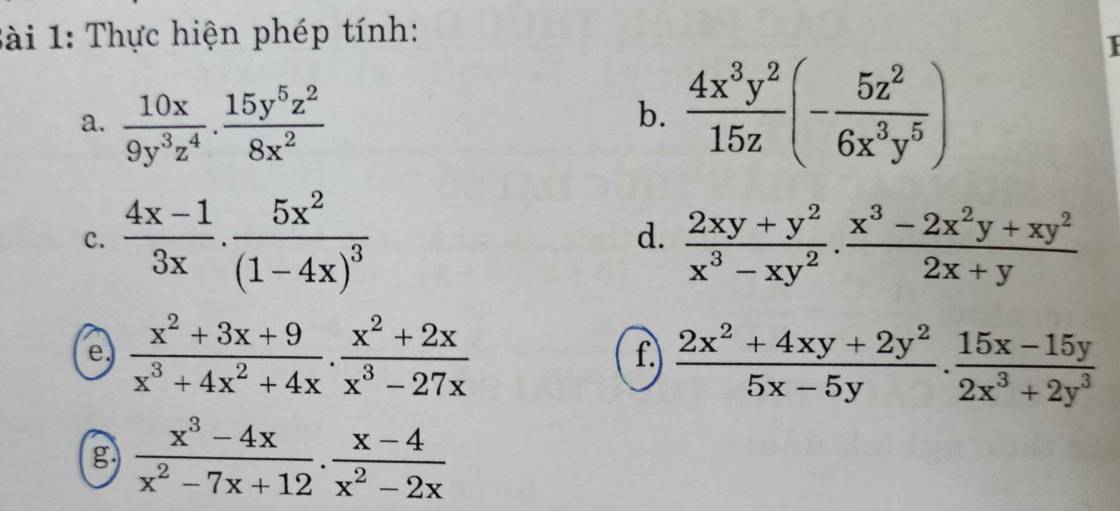 giúp e mấy câu khoanh vs ạ 🥲
giúp e mấy câu khoanh vs ạ 🥲
e: \(\dfrac{x^2+3x+9}{x^3+4x^2+4x}\cdot\dfrac{x^2+2x}{x^3-27x}\)
\(=\dfrac{x^2+3x+9}{x\left(x^2+4x+4\right)}\cdot\dfrac{x\left(x+2\right)}{x\left(x^2-27\right)}\)
\(=\dfrac{x^2+3x+9}{\left(x+2\right)^2}\cdot\dfrac{x+2}{x\left(x^2-27\right)}\)
\(=\dfrac{\left(x^2+3x+9\right)}{\left(x+2\right)\cdot x\left(x^2-27\right)}\)
f: \(\dfrac{2x^2+4xy+2y^2}{5x-5y}\cdot\dfrac{15x-15y}{2x^3+2y^3}\)
\(=\dfrac{2\left(x^2+2xy+y^2\right)}{5\left(x-y\right)}\cdot\dfrac{15\left(x-y\right)}{2\left(x^3+y^3\right)}\)
\(=\dfrac{\left(x+y\right)^2}{1}\cdot\dfrac{3}{\left(x+y\right)\left(x^2-xy+y^2\right)}\)
\(=\dfrac{3\left(x+y\right)}{x^2-xy+y^2}\)
g: \(\dfrac{x^3-4x}{x^2-7x+12}\cdot\dfrac{x-4}{x^2-2x}\)
\(=\dfrac{x\left(x^2-4\right)}{\left(x-3\right)\left(x-4\right)}\cdot\dfrac{x-4}{x\left(x-2\right)}\)
\(=\dfrac{x^2-4}{\left(x-3\right)\left(x-2\right)}=\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-3\right)\left(x-2\right)}=\dfrac{x+2}{x-3}\)
Đúng 2
Bình luận (2)
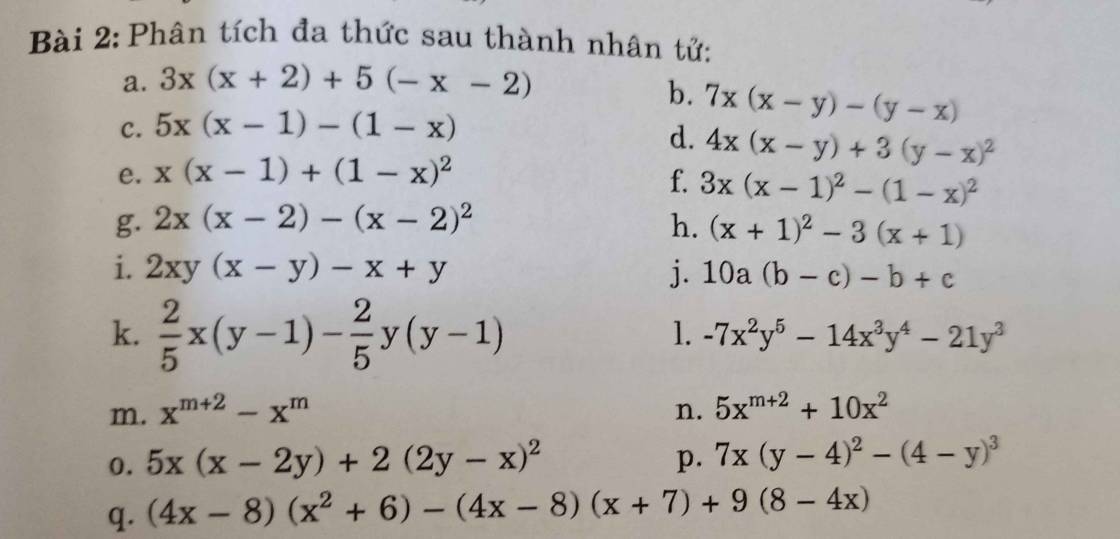 giúp e từ câu m đến q vs ạ 🥲
giúp e từ câu m đến q vs ạ 🥲
m: \(=x^m\cdot x^2-x^m=x^m\left(x^2-1\right)=x^m\left(x-1\right)\left(x+1\right)\)
n: \(=5\cdot x^m\cdot x^2+10x^2\)
\(=5x^2\left(x^m+2\right)\)
o: \(=5x\left(x-2y\right)+2\left(x-2y\right)^2\)
\(=\left(x-2y\right)\left(5x+2x-4y\right)\)
=(x-2y)(7x-4y)
p: \(=7x\left(y-4\right)^2+\left(y-4\right)^3\)
\(=\left(y-4\right)^2\cdot\left(7x+y-4\right)\)
q: \(\left(4x-8\right)\left(x^2+6\right)-\left(4x-8\right)\left(x+7\right)+9\left(8-4x\right)\)
\(=\left(4x-8\right)\left(x^2+6-x-7\right)-9\left(4x-8\right)\)
\(=\left(4x-8\right)\left(x^2-x-10\right)\)
\(=4\left(x-2\right)\left(x^2-x-10\right)\)
Đúng 1
Bình luận (1)
m) \(x^{m+2}-x^m\)
\(=x^m\cdot x^2-x^m\)
\(=x^m\left(x^2-1\right)\)
\(=x^m\left(x^2-1^2\right)\)
\(=x^m\left(x-1\right)\left(x+1\right)\)
n) \(5x^{m+2}+10x^2\)
\(=5x^m\cdot x^2+10x^2\)
\(=5x^2\cdot x^m+10x^2\)
\(=5x^2\left(x^m+2\right)\)
o) \(5x\left(x-2y\right)+2\left(2y-x\right)^2\)
\(=5x\left(x-2y\right)+2\left(x-2y\right)^2\)
\(=\left(x-2y\right)\left[5x+2\left(x-2y\right)\right]\)
\(=\left(x-2y\right)\left(5x+2x-4y\right)\)
\(=\left(x-2y\right)\left(7x-4y\right)\)
p) \(7x\left(y-4\right)^2-\left(4-y\right)^3\)
\(=7x\left(4-y\right)^2-\left(4-y\right)^3\)
\(=\left(4-y\right)^2\left[7x-\left(4-y\right)\right]\)
\(=\left(4-y\right)^2\left(7x-4+y\right)\)
q) \(\left(4x-8\right)\left(x^2+6\right)-\left(4x-8\right)\left(x+7\right)+9\left(8-4x\right)\)
\(=4\left(x-2\right)\left(x^2+6\right)-4\left(x-2\right)\left(x+7\right)-36\left(x-2\right)\)
\(=4\left(x-2\right)\left[\left(x^2+6\right)-\left(x+7\right)-9\right]\)
\(=4\left(x-2\right)\left(x^2+6-x-7-9\right)\)
\(=4\left(x-2\right)\left(x^2-x-10\right)\)
Đúng 1
Bình luận (1)
Giúp e vs ạ , e chx hiểu lắm .
Đọc tiếp
Giúp e vs ạ , e chx hiểu lắm .
Bài 7:
a: a>b
nên -2a<-2b
=>-2a-6<-2b-6<-2b
b: a>b
nên 3a>3b
=>3a-9>3b-9
=>3(a-3)>3(b-3)
Đúng 1
Bình luận (0)
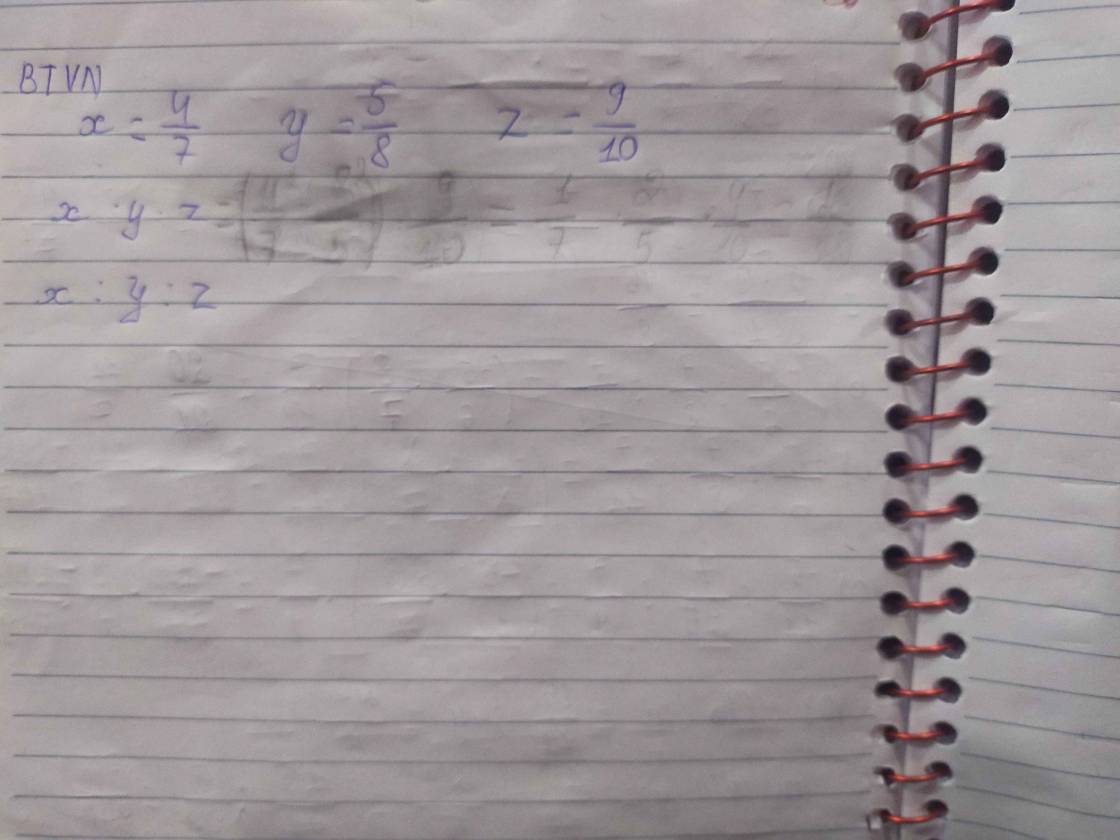 giúp e vs ạ 🥲
giúp e vs ạ 🥲
\(x:y:z=\dfrac{4}{7}:\dfrac{5}{8}:\dfrac{9}{10}=160:175:252\)
Đúng 1
Bình luận (0)
 giúp e vs ạ 🥲
giúp e vs ạ 🥲
 giúp e vs ạ 🥲
giúp e vs ạ 🥲
\(4x^4+1\)
\(=4x^4+4x^2+1-4x^2\)
\(=\left(2x^2+1\right)^2-\left(2x\right)^2\)
\(=\left(2x^2+1+2x\right)\left(2x^2+1-2x\right)\)
Đúng 2
Bình luận (0)
\(4x^4+1=4x^4+4x^2+1-4x^2=\left(2x^2+1\right)^2-\left(2x\right)^2\)
\(=\left(2x^2-2x+1\right)\left(2x^2+2x+1\right)\)
Đúng 2
Bình luận (0)
Giúp e bài 4 vs ạ(có vẽ hình),e cần cách lm dễ hiểu chi tiết,bài này e cần lắm luôn đó ạ nên giúp e lm đúng vs(nếu mn có thời gian thì giúp e luôn bài 2 vs,e ko đc chắc chắn bài này e lm có đúng ko)e cảm ơn nhìu lắm ạ!!!
Bài 2: Chọn C
Bài 4:
a: \(\widehat{C}=180^0-80^0-50^0=50^0\)
Xét ΔABC có \(\widehat{A}=\widehat{C}< \widehat{B}\)
nên BC=AB<AC
b: Xét ΔABC có AB<BC<AC
nên \(\widehat{C}< \widehat{A}< \widehat{B}\)
Đúng 1
Bình luận (0)
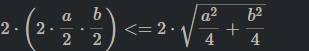
Gthich bước này chi tiết giúp e vs, e kh hiểu lắm ạ
Cái chỗ này mình xin lỗi bạn nhiều nha, mình bị sai chỗ này rồi
Ta có: \(\left(a-b\right)^2>=0\forall a,b\)
=>\(a^2+b^2-2ab>=0\forall a,b\)
=>\(a^2+b^2>=2ab\forall a,b\)
Dấu "=" xảy ra khi a=b
\(2\cdot\left(\dfrac{a}{2}\cdot\dfrac{b}{2}\right)< =\left(\dfrac{a}{2}\right)^2+\left(\dfrac{b}{2}\right)^2=\dfrac{a^2+b^2}{4}\)
=>\(2\cdot\left(2\cdot\dfrac{a}{2}\cdot\dfrac{b}{2}\right)< =\dfrac{2\left(a^2+b^2\right)}{4}=\dfrac{a^2+b^2}{2}\)
Bạn bỏ giúp mình dấu căn nha
Đúng 0
Bình luận (1)




