1/Cho (O) đường kính CD. Lấy K thuộc bán kính OC; vẽ dây AB vuông góc OC tại K. Tiếp tuyến B cắt OC tại M. C/m tam giác MBC đồng dạng tam giác MDB
2/ Giải phương trình \(\sqrt{\left(x-1\right)^2-\left(x^2-3\right)}=3\)
TP
Những câu hỏi liên quan
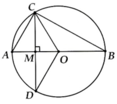
Bài : Cho đường kính CD . Lấy điểm K tùy ý thuộc bán kính OC , vẽ dây AB vuông góc OC tại K . Tiếp tuyến tại b cắt tia OC tại M . Ch.minh
a) OK là phân giác của góc AOB
b) MA là tiếp tuyến của (O)
c) tam giác MBC đồng dạng tam giác MDB
a: ΔOAB cân tại O
mà OK là đường cao
nên OK là phân giác của \(\widehat{AOB}\)
b: Xét ΔOAM và ΔOBM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔOAM=ΔOBM
=>\(\widehat{OAM}=\widehat{OBM}=90^0\)
=>AM là tiếp tuyến của (O)
c: Xét ΔMBC và ΔMDB có
\(\widehat{MBC}=\widehat{MDB}\left(=\dfrac{1}{2}sđ\stackrel\frown{MB}\right)\)
\(\widehat{BMC}\) chung
Do đó: ΔMBC đồng dạng với ΔMDB
Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính AB; trên nửa đường tròn lấy điểm C sao cho AC>AB, qua C dựng đường thẳng vuông góc với OC cắt đường thẳng AB tại D. Kẻ CH vuông góc với AB (H thuộc AB), kẻ BK vuông góc với CD ( K thuộc CD); đường kính CH cắt đường thẳng BK tại E. a) Chứng minh 4 điểm C,H,B,K cùng thuộc 1 đường tròn. b) Cm KH//AC. c) Cm BH.AD=AH.BD
a: Ta có: \(\widehat{CHB}=90^0\)
=>ΔCHB vuông tại H
=>ΔCHB nội tiếp đường tròn đường kính CB(4)
Ta có: \(\widehat{CKB}=90^0\)
=>ΔCKB vuông tại K
=>ΔCKB nội tiếp đường tròn đường kính CB(5)
Từ (4) và (5) suy ra C,H,B,K cùng thuộc đường tròn đường kính CB
b:
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Ta có: \(\widehat{OCB}+\widehat{BCK}=\widehat{OCK}=90^0\)
\(\widehat{OCB}+\widehat{OCA}=\widehat{BCA}=90^0\)
Do đó: \(\widehat{BCK}=\widehat{OCA}\)(1)
Ta có: CHBK là tứ giác nội tiếp
=>\(\widehat{BCK}=\widehat{BHK}\left(2\right)\)
Xét ΔOAC có OC=OA
nên ΔOAC cân tại O
=>\(\widehat{OAC}=\widehat{OCA}\)(3)
Từ (1),(2),(3) suy ra \(\widehat{BHK}=\widehat{OAC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên HK//AC
Đúng 1
Bình luận (0)
vẽ hộ hình giúp mình với phần a) Cm 2 tam giác nội tiếp
Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính AB; trên nửa đường tròn lấy điểm C sao cho AC>AB, qua C dựng đường thẳng vuông góc với OC cắt đường thẳng AB tại D. Kẻ CH vuông góc với AB (H thuộc AB), kẻ BK vuông góc với CD ( K thuộc CD); đường kính CH cắt đường thẳng BK tại E. Chứng mình 4 điểm C,H,B,K cùng thuộc 1 đường tròn'
Xét tứ giác CHBK có
\(\widehat{CHB}+\widehat{CKB}=90^0+90^0=180^0\)
=>CHBK là tứ giác nội tiếp
=>C,H,B,K cùng thuộc một đường tròn
Đúng 0
Bình luận (1)
Cho đường tròn (O) đường kính AB. Lấy M thuộc đoạn AB. vẽ dây CD vuông góc với AB tại M. Giả sử AM 2cm và CD
4
3
cm. Tính:a, Độ dài đường tròn (O) và diện tích đường tròn (O)b, Độ dài cung
C
A
D
⏜
và diện tích hình quạt tròn giói hạn bởi hai bán kính OC, OD và cung nhỏ
C...
Đọc tiếp
Cho đường tròn (O) đường kính AB. Lấy M thuộc đoạn AB. vẽ dây CD vuông góc với AB tại M. Giả sử AM = 2cm và CD = 4 3 cm. Tính:
a, Độ dài đường tròn (O) và diện tích đường tròn (O)
b, Độ dài cung C A D ⏜ và diện tích hình quạt tròn giói hạn bởi hai bán kính OC, OD và cung nhỏ C D ⏜
a, AC = 4cm => BC = 4 3 cm
=> R = 4cm => C = 8πcm, S = 16π c m 2
b, ∆AOC đều => A O C ^ = 60 0
=> C O D ^ = 120 0 => l C A D ⏜ = π . 4 . 120 180 = 8 π 3 cm
=> S = 8 π 3 . 4 2 = 16 π 3 c m 2
Đúng 1
Bình luận (0)
Cho nửa đường tròn (O) đường kính AB và bán kính OC ⊥ AB. Lấy điểm M thuộc cung AC . Tiếp tuyến tại M cắt OC tại N. Chứng minh rằng MNO = 2MBA
Cho nửa đường tròn (O) đường kính AB và bán kính OC ⊥ AB. Lấy điểm M thuộc cung AC . Tiếp tuyến tại M cắt OC tại N. Chứng minh rằng góc MNO = 2 góc MBA
Cho nửa (O). Đường kính AB. Trên nửa mặt phẳng bờ AB vẽ các tiếp tuyến Ax, By với (O). Lấy C thuộc Ax. Vẽ OD vuông góc với OC (D thuộc By):
- Cho bán kính (O) là R. Góc ACD = 120 độ. Tính AC, BD, CD theo R.
- Xác định vị trí của C để AC + BD đạt giá trị nhỏ nhất.
1. Cho nữa đường tròn (O), đường kính AB & C thuộc nửa đường tròn . Trên bán kính OC lấy điểm D sao cho OD=CH ( CH vuông góc AB, H thuộc AB) . Khi C chạy trên nửa đường tròn thì D chạy trên đường nào
Trên dây cung AB của đường tròn (O) lấy hai điểm H và K sao cho AH= HK = KB. Vẽ bán kính OD qua H và bán kính OC qua K. Chứng minh rằng:1)Cung AD = cung BC 2) Cung AD < cung DC


