Tìm GTNN hoặc GTLN của:
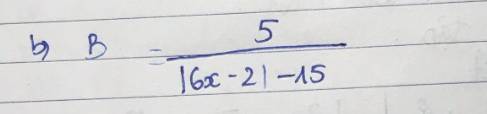
Tìm GTNN hoặc GTLN của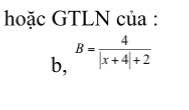
\(\left|x+4\right|+2\ge2\forall x\)
nên \(B\le\dfrac{4}{2}=2\forall x\)
Dấu '=' xảy ra khi x=-4
Tìm GTLN hoặc GTNN của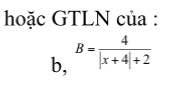
Tìm GTNN hoặc GTLN của: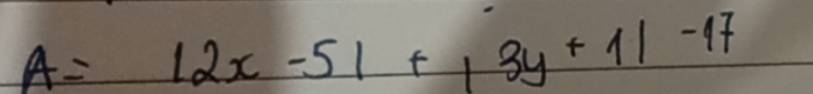
Ta thấy:
\(\left|2x-5\right|\ge0\forall x\)
\(\left|3y+1\right|\ge0\forall y\)
\(\Rightarrow\left|2x-5\right|+\left|3y+1\right|\ge0\forall x;y\)
\(\Rightarrow A=\left|2x-5\right|+\left|3y+1\right|-17\ge-17\forall x;y\)
Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}2x-5=0\\3y+1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=-\dfrac{1}{3}\end{matrix}\right.\)
Vậy \(Min_A=-17\) khi \(x=\dfrac{5}{2};y=-\dfrac{1}{3}\).
\(\left|2x-5\right|>=0\forall x;\left|3y+1\right|>=0\forall y\)
=>\(\left|2x-5\right|+\left|3y+1\right|>=0\forall x,y\)
=>\(A=\left|2x-5\right|+\left|3y+1\right|-17>=-17\)
Dấu = xảy ra khi \(\left\{{}\begin{matrix}2x-5=0\\3y+1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=-\dfrac{1}{3}\end{matrix}\right.\)
Tìm GTNN hoặc GTLN của:
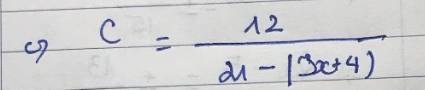
c) \(C=\dfrac{12}{21-\left|3x+4\right|}\left(dkxd:x\ne\dfrac{17}{3};x\ne-\dfrac{25}{3}\right)\)
Ta thấy: \(\left|3x+4\right|\ge0\)
\(\Rightarrow-\left|3x+4\right|\le0\forall x\)
\(\Rightarrow21-\left|3x+4\right|\le21\forall x\)
\(\Rightarrow\dfrac{1}{21-\left|3x+4\right|}\ge\dfrac{1}{21}\forall x\)
\(\Rightarrow C=\dfrac{12}{21-\left|3x+4\right|}\ge\dfrac{12}{21}=\dfrac{4}{7}\forall x\)
Dấu \("="\) xảy ra khi: \(3x+4=0\Leftrightarrow x=-\dfrac{4}{3}\left(tm\right)\)
Vậy \(Min_C=\dfrac{4}{7}\) khi \(x=-\dfrac{4}{3}\).
c) C = 12 21 − | 3 x + 4 | ( d k x d : x ≠ 17 3 ; x ≠ − 25 3 ) Ta thấy: | 3 x + 4 | ≥ 0 ⇒ − | 3 x + 4 | ≤ 0 ∀ x ⇒ 21 − | 3 x + 4 | ≤ 21 ∀ x ⇒ 1 21 − | 3 x + 4 | ≥ 1 21 ∀ x ⇒ C = 12 21 − | 3 x + 4 | ≥ 12 21 = 4 7 ∀ x Dấu "=" xảy ra khi: 3 x + 4 = 0 ⇔ x = − 4 3 ( t m ) Vậy M i n C = 4 7 khi x = − 4 3 .
tìm gtln hoặc gtnn của A= 2021-x/11-x
\(A=\dfrac{2021-x}{11-x}=\dfrac{11-x+2010}{11-x}=\dfrac{11-x}{11-x}+\dfrac{2010}{11-x}=1+\dfrac{2010}{11-x}\)
Để A đạt GTNN thì \(\dfrac{2010}{11-x}\) nhỏ nhất
\(\Rightarrow11-x=2010\Leftrightarrow x=-1999\)
Khi đó \(A=2\)
Để A đạt GTLN thì \(\dfrac{2010}{11-x}\) lớn nhất
\(\Rightarrow11-x=1\Leftrightarrow x=10\)
Khi đó \(A=2011\)
Vậy \(Min_A=2\) khi \(x=-1999\) và \(Max_A=2011\) khi \(x=10\)
tìm GTLN hoặc GTNN của 6n-3/4n-6
Tìm GTNN hoặc GTLN của:
a) A=|2x-1|-4 (GTLN)
b) B = 1,5-|2-x| (GTLN)
c) C = |x-3|(GTNN)
d)D = 10-4|x-2|(GTLN)
a) Sửa đề: Tìm GTNN
A = |2x - 1| - 4
Ta có:
|2x - 1| ≥ 0 với mọi x ∈ R
⇒ |2x - 1| - 4 ≥ -4 với mọi x ∈ R
Vậy GTNN của A là -4 khi x = 1/2
b) B = 1,5 - |2 - x|
Ta có:
|2 - x| ≥ 0 với mọi x ∈ R
⇒ -|2 - x| ≤ 0 với mọi x ∈ R
⇒ 1,5 - |2 - x| ≤ 1,5 với mọi x ∈ R
Vậy GTLN của B là 1,5 khi x = 2
c) C = |x - 3| ≥ 0 với mọi x ∈ R
Vậy GTNM của C là 0 khi x = 3
d) D = 10 - 4|x - 2|
Ta có:
|x - 2| ≥ 0 với mọi x ∈ R
⇒ 4|x - 2| ≥ 0 với mọi x ∈ R
⇒ -4|x - 2| ≤ 0 với mọi x ∈ R
⇒ 10 - 4|x - 2| ≤ 10 với mọi x ∈ R
Vậy GTLN của D là 10 khi x = 2
Tìm GTNN hoặc GTLN của D= x- x^2+3
D = x - x2 + 3
D = - x2 + x + 3
D = - ( x2 - x - 3 )
D = - [ x2 - 2 . x . 1 / 2 + ( 1 / 2 )2 - ( 1 / 2 )2 - 3 ]
D = - [ ( x - 1 / 2 )2 - 13 / 4 ]
D = - ( x - 1 / 2 )2 + 13 / 4 \(\le\)13 / 4
Dấu " = " xảy ra \(\Leftrightarrow\)x - 1 / 2 = 0
\(\Rightarrow\)x = 1 / 2
Max D = 13 / 4 \(\Leftrightarrow\)x = 1 / 2
D=x-x^2+3
D= -[x^2 -x +1/4 ] + 13/4
D=-(x-1/2)^2 +13/4
Vì -(x-1/2)^2<=0 => D<=13/4
Dấu = xảy ra <=> x-1/2=0 <=> x=1/2
\(D=x-x^2+3\)
\(D=-\left(x^2-x+3\right)\)
\(D=-\left(x^2-x+\frac{1}{4}+\frac{11}{4}\right)\)
\(D=-\left[\left(x-\frac{1}{2}\right)^2+\frac{11}{4}\right]\)
\(D=-\left(x-\frac{1}{2}\right)^2-\frac{11}{4}\le\frac{-11}{4}\)
Dấu bằng xảy ra
\(\Leftrightarrow x-\frac{1}{2}=0\)
\(\Leftrightarrow x=\frac{1}{2}\)
Vậy Max \(D=\frac{-11}{4}\)\(\Leftrightarrow x=\frac{1}{2}\)
Tìm GTNN hoặc GTLN của C= x^2- 4x+ 8
\(C=x^2-4x+8\)
\(C=x^2-4x+4+4\)
\(C=\left(x-4\right)^2+4\ge4\)
Dấu bằng xảy ra
\(\Leftrightarrow x-4=0\)
\(\Leftrightarrow x=4\)
Vậy Min A = 4 <=> x= 4
giải lun câu này dùm ik: D= x- x^2+ 3. Tìm GTNN hoặc GTLN