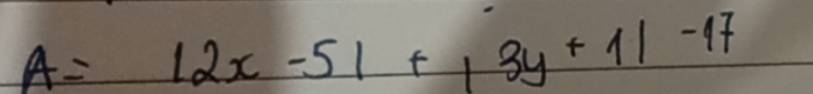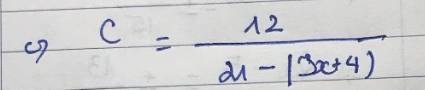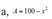Ta thấy:
\(\left|2x-5\right|\ge0\forall x\)
\(\left|3y+1\right|\ge0\forall y\)
\(\Rightarrow\left|2x-5\right|+\left|3y+1\right|\ge0\forall x;y\)
\(\Rightarrow A=\left|2x-5\right|+\left|3y+1\right|-17\ge-17\forall x;y\)
Dấu \("="\) xảy ra khi: \(\left\{{}\begin{matrix}2x-5=0\\3y+1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=-\dfrac{1}{3}\end{matrix}\right.\)
Vậy \(Min_A=-17\) khi \(x=\dfrac{5}{2};y=-\dfrac{1}{3}\).
\(\left|2x-5\right|>=0\forall x;\left|3y+1\right|>=0\forall y\)
=>\(\left|2x-5\right|+\left|3y+1\right|>=0\forall x,y\)
=>\(A=\left|2x-5\right|+\left|3y+1\right|-17>=-17\)
Dấu = xảy ra khi \(\left\{{}\begin{matrix}2x-5=0\\3y+1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=-\dfrac{1}{3}\end{matrix}\right.\)