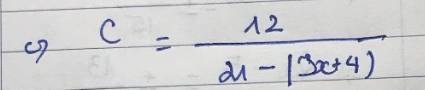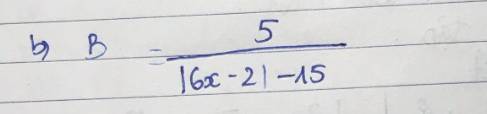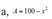c) \(C=\dfrac{12}{21-\left|3x+4\right|}\left(dkxd:x\ne\dfrac{17}{3};x\ne-\dfrac{25}{3}\right)\)
Ta thấy: \(\left|3x+4\right|\ge0\)
\(\Rightarrow-\left|3x+4\right|\le0\forall x\)
\(\Rightarrow21-\left|3x+4\right|\le21\forall x\)
\(\Rightarrow\dfrac{1}{21-\left|3x+4\right|}\ge\dfrac{1}{21}\forall x\)
\(\Rightarrow C=\dfrac{12}{21-\left|3x+4\right|}\ge\dfrac{12}{21}=\dfrac{4}{7}\forall x\)
Dấu \("="\) xảy ra khi: \(3x+4=0\Leftrightarrow x=-\dfrac{4}{3}\left(tm\right)\)
Vậy \(Min_C=\dfrac{4}{7}\) khi \(x=-\dfrac{4}{3}\).
c) C = 12 21 − | 3 x + 4 | ( d k x d : x ≠ 17 3 ; x ≠ − 25 3 ) Ta thấy: | 3 x + 4 | ≥ 0 ⇒ − | 3 x + 4 | ≤ 0 ∀ x ⇒ 21 − | 3 x + 4 | ≤ 21 ∀ x ⇒ 1 21 − | 3 x + 4 | ≥ 1 21 ∀ x ⇒ C = 12 21 − | 3 x + 4 | ≥ 12 21 = 4 7 ∀ x Dấu "=" xảy ra khi: 3 x + 4 = 0 ⇔ x = − 4 3 ( t m ) Vậy M i n C = 4 7 khi x = − 4 3 .