cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AB. Gọi M,N lần lượt là trung điểm SA,SC; E = AC giao BD. Xác định vị trí tương đối của các cặp đường thẳng và mặt phẳng sau
a) MN và (ABCD)
b) AN và (ABD)
c) SE và (SAC)
Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi M, N lần lượt là trung điểm của SA, SB. Gọi P là giao điểm của SC và (AND). AN cắt DP tại I. SABI là hình gì?
A. Hình bình hành
B. Hình chữ nhật
C. Hình vuông
D. Hình thoi
Đáp án A
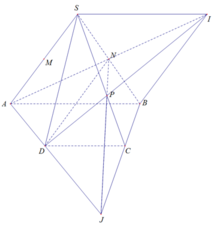
Xét (ABCD) có: A D ∩ B C = J
J ∈ BC ⇒ J ∈ (SBC)
Xét (SBC), Kẻ JN cắt SC tại P
Xét (SAB) và (SCD) có :
S là điểm chung
AB // CD
⇒ Giao tuyến là đường thẳng song song với AB
Mà I = A N ∩ D P
AN ⊂ (SAB)
DP ⊂ (SCD)
⇒ I nằm trên giao tuyến của 2 mặt phẳng
⇒ SI // AB
⇒ ASIB là hình thang có: SN = NB ( N là trung điểm SB)
⇒ ASIB là hình bình hành
1) cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AB, E = AC, AC giao BD. Gọi M,N lần lượt là trung điểm SA,SC. Xét vị trí tương đối của
a) BD và AC
b) MN và AC
c) MN và SE
d) Tìm giao điểm của SN và mp (ABCD)
a: BD cắt AC tại E
b: Xét ΔSAC có SM/SA=SN/SC
nên MN//AC
c: Trong mp(SAC), ta có: SE không song song với MN
=>SE cắt MN tại K
d: \(C\in SN\)
\(C\in\left(ABCD\right)\)
Do đó: \(SN\cap\left(ABCD\right)=C\)
Cho hình chóp S.ABCD có đáy là hình thang ABCD (đáy lớn AB). Gọi E, F lần lượt là trung điểm của SA và SB. Chứng minh EF // CD
Ta có: `EF` là đường trung bình của tam giác `ABC` nên `EF`//`AB`
`ABCD` là hình thang => `CD`//`AB`
Do đó: `EF`//`CD` `(đpcm)`
cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AB. Gọi M,N lần lượt là trung điểm SA, SC, E = AC giao BD.
a) tìm giao tuyến của 2 mặt phẳng (SAC) và (SBD)
b) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
c) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
a: \(E\in AC\subset\left(SAC\right)\)
\(E\in BD\subset\left(SBD\right)\)
Do đó: \(E\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SE\)
b: Gọi K là giao của AD với BC
\(K\in AD\subset\left(SAD\right)\)
\(K\in BC\subset\left(SBC\right)\)
Do đó: \(K\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(SK=\left(SAD\right)\cap\left(SBC\right)\)
c: AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó: \(\left(SAB\right)\cap\left(SCD\right)=xy\), xy đi qua S và xy//AB//CD
cho hình chóp S.ABCD, đáy ABCD là hình thang, có đáy lớn AB. Gọi M,N lần lượt là trung điểm SA, SC, E = AC giao BD.
a) tìm giao tuyến của 2 mặt phẳng (SAC) và (SBD)
b) tìm giao tuyến của 2 mặt phẳng (SAD) và (SBC)
c) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
a: \(E\in AC\subset\left(SAC\right);E\in BD\subset\left(SBD\right)\)
=>\(E\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SE\)
b: Gọi K là giao của AD và BC
\(K\in AD\subset\left(SAD\right);K\in BC\subset\left(SBC\right)\)
=>\(K\in\left(SAD\right)\cap\left(SBC\right)\)
mà \(S\in\left(SAD\right)\cap\left(SBC\right)\)
nên \(\left(SAD\right)\cap\left(SBC\right)=SK\)
c: Xét (SAB) và (SCD) có
AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó: (SAB) giao (SCD)=xy; xy đi qua S và xy//AB//CD
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật, A B = S A = a , A D = a 2 , S A vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AD và SC, gọi I là giao điểm của BM và AC. Tỷ số V A M N I V S . A B C D là?
A. 1/24
B. 1/12
C. 1/6
D.1/7
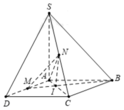
Đáp án A
Vì A M / / B C ⇒ I M I B = M A B C = 1 2 ⇒ d I ; A D d B ; A D = 1 3
|
Suy ra S Δ I M A = 1 2 d I ; A D . A M = 1 2 . 1 3 d B ; A D . 1 2 A D = S A B C D 12
Mà N là trung điểm của S C ⇒ d N ; A B C D = 1 2 d S ; A B C D
Vậy V A M N I V S . A B C D = d N ; A B C D d S ; A B C D . S Δ I M A S A B C D = 1 2 . 1 12 = 1 24
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC. Biết thể tích của khối chóp S.BMN là a 3 . Tính thể tích khối chóp S.ABCD
A. a 3
B. 4 a 3
C. 8 a 3
D. 16 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M, N lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng tứ giác MNCD là hình thang.
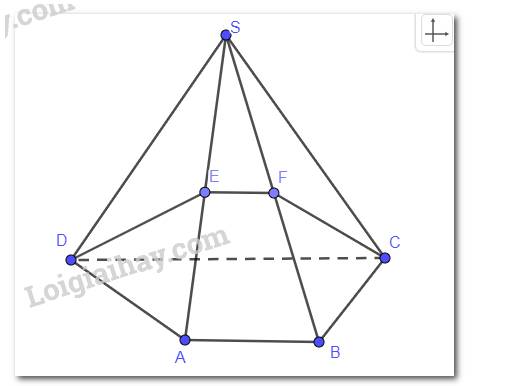
Xét tam giác SAB ta có MN là đường trung bình suy ra MN // AB.
Mà AB // CD do đó MN // CD.
Suy ra MNCD là hình thang.
Cho hình chóp SABCD có đáy ABCD là hình thang với AB//CD. Gọi M,N,P,Q lần lượt là trung điểm của SD,SC,SB,SA. Chứng minh (MNPQ)//(ABCD)
Do M là trung điểm SD, N là trung điểm SC \(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow MN||CD\) (1)
Tương tự PQ là đường trung bình tam giác SAB \(\Rightarrow PQ||AB\)
\(\Rightarrow MN||PQ\Rightarrow\) 4 điểm M, N, P, Q đồng phẳng
Lại có MQ là đường trung bình tam giác SAD \(\Rightarrow MQ||AD\)
Mà \(AD\in\left(ABCD\right)\Rightarrow MQ||\left(ABCD\right)\)
Do \(CD\in\left(ABCD\right)\), từ \(\left(1\right)\Rightarrow MN||\left(ABCD\right)\)
Mà \(\left\{{}\begin{matrix}MN\in\left(MNPQ\right)\\MQ\in\left(MNPQ\right)\\MN\cap MQ=M\end{matrix}\right.\)\(\Rightarrow\left(MNPQ\right)||\left(ABCD\right)\)